C#实现马尔科夫模型例子

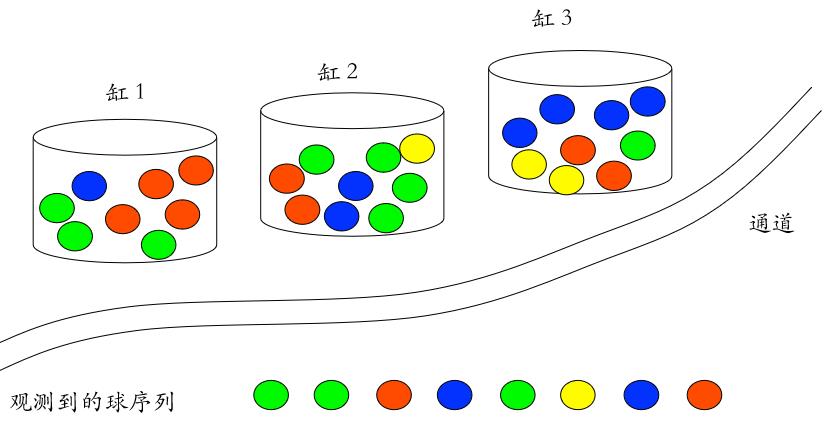
已知条件：三个缸N状态，每个缸中不同颜色球的个数M状态值，时间轴T，观察值序列O

参数：状态值序列，转移概率序列

求：概率

后台代码如下

         const int N = , M = ;//N状态，M状态值 (0橙色，1绿色，2蓝色，3黄色)
         public int[] O = { , , , , , , ,  };//观察值序列
         public double[,] A = new double[N, N];//初始一个三行三列的二维数组(状态转移概率)
         public double[,] B = new double[N, M];//初始一个三行四列的二维数组（观察值的概率矩阵）
         public double[] PI = { 1.0 / 3.0, 1.0 / 3.0, 1.0 / 3.0 };//初始化概率
         #region 获取观察值概率
         /// <summary>
         /// 获取观察值概率
         /// </summary>
         public void GetB()
         {
             //第一缸球的颜色
             double[] one = { , , ,  };
             //第二缸球的颜色
             double[] two = { , , ,  };
             //第一缸球的颜色
             double[] three = { , , ,  };
             //每个缸中球的总数量
             int[] count = { , ,  };
             for (int i = ; i < ; i++)
             {
                 B[, i] = one[i] / count[];
                 B[, i] = two[i] / count[];
                 B[, i] = three[i] / count[];
             }
         }
         #endregion

         #region 获取概率P值 zhy
         /// <summary>
         /// 获取概率P值
         /// </summary>
         /// <param name="Q">状态值序列(0第一个缸，1第二个缸，2第三个缸)</param>
         /// <param name="A">转移概率</param>
         /// <returns></returns>
         public double GetP(string Q, string A)
         {
             GetA(A);
             GetB();
             int[] q = GetQ(Q);
             //时间轴
             int T = ;
             //初始概率Q[0]：第一缸， O[0]：第一个球
             double p = PI[q[]] * B[q[], O[]];
             for (int i = ; i < T; i++)
             {
                 //this.A:q[i-1]取上一个刚，q[i]取当前缸，然后获得转移概率
                 //B:q[i]取当前缸，O[i]取缸中哪个颜色的球
                 p *= this.A[q[i - ], q[i]] * B[q[i], O[i]];
             }
             return p;
         }
         #endregion

         #region 获取状态值序列 zhy
         /// <summary>
         /// 获取状态值序列
         /// </summary>
         /// <param name="Q">状态值字符串</param>
         /// <returns>状态值数组</returns>
         public int[] GetQ(string Q)
         {
             int[] q = null;
             if (Q.TrimEnd(',').IndexOf(',') > )
             {
                 //获得状态序列
                 string[] zhuangtai = Q.TrimEnd(',').Split(',');
                 q = new int[zhuangtai.Length];
                 for (int i = ; i < zhuangtai.Length; i++)
                 {
                     q[i] = Convert.ToInt32(zhuangtai[i]);
                 }
             }
             else
             {
                 q = new int[];
                 q[] = Convert.ToInt32(Q);
             }
             return q;
         }
         #endregion

         #region 获取转移概率序列 zhy
         /// <summary>
         /// 获取转移概率序列
         /// </summary>
         /// <param name="A">转移概率字符串</param>
         public void GetA(string A)
         {
             if (A.TrimEnd(',').IndexOf(',') > )
             {
                 string[] gailv = A.TrimEnd(',').Split(',');
                 //获取A的转移概率的二维数组
                 for (int i = ; i < ; i++)
                 {
                     for (int j = ; j < ; j++)
                     {
                         this.A[i, j] = Convert.ToDouble(gailv[ * i + j]);
                     }
                 }
             }
         }
         #endregion

html如下：

         <span>请输入状态值序列&nbsp;&nbsp;： </span><input type="text" id="zhuangtaizhi" value="0,2,1,1,2,0,0,1" /><span>&nbsp;&nbsp; 多个值请使用","隔开（0第一缸，1第二缸，2第三缸）</span><br /><br />
         <span>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; a11-a13  ：</span>
         <input type="text" id="a11_a13" value="0.25,0.45,0.2" /><span>&nbsp;&nbsp; 请输入第一缸的转移概率以","隔开,三值相加等于1</span><br /><br />
         <span>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; a21-a23  ：</span>
         <input type="text" id="a21_a23" value="0.1,0.85,0.15" /><span>&nbsp;&nbsp; 请输入第二缸的转移概率以","隔开,三值相加等于1</span><br /><br />
         <span>&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp; a31-a33  ：</span>
         <input type="text" id="a31_a33" value="0.14,0.55,0.31" /><span>&nbsp;&nbsp; 请输入第三缸的转移概率以","隔开,三值相加等于1</span><br /><br />
         &nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;
         <input type="button" value="计算" onclick="count()" />
         <div style="display:none;" id="jieguo">
             <span>概率为：</span><span id="gailv"></span>
         </div>

js如下

 function count() {
         var zhuangtaizhi = $.trim($("#zhuangtaizhi").val());
         var a11_a13 = $.trim($("#a11_a13").val());
         var a21_a23 = $.trim($("#a21_a23").val());
         var a31_a33 = $.trim($("#a31_a33").val());
         if (zhuangtaizhi == "") {
             alert("请输入状态值序列");
             return;
         }
         if (a11_a13 == "") {
             alert("请输入a11-a13的转移概率");
             return;
         }
         if (a21_a23 == "") {
             alert("请输入a21-a23的转移概率");
             return;
         }
         if (a21_a23 == "") {
             alert("请输入a21-a23的转移概率");
             return;
         }
         var zhuanyigailv = a11_a13 + "," + a21_a23 + "," + a31_a33;
         $.post("/YinMa/GetP", { Q: zhuangtaizhi, A: zhuanyigailv }, function (msg) {
             $("#gailv").html(msg);
             $("#jieguo").show();
         });
     }

纯本人手写，转载请注明出处