luoguP3690 【模板】Link Cut Tree （动态树）[LCT]

题目背景

动态树

题目描述

给定Ｎ个点以及每个点的权值，要你处理接下来的Ｍ个操作。操作有４种。操作从０到３编号。点从１到Ｎ编号。

０：后接两个整数（ｘ，ｙ），代表询问从ｘ到ｙ的路径上的点的权值的ｘｏｒ和。保证ｘ到ｙ是联通的。

１：后接两个整数（ｘ，ｙ），代表连接ｘ到ｙ，若ｘ到Ｙ已经联通则无需连接。

２：后接两个整数（ｘ，ｙ），代表删除边（ｘ，ｙ），不保证边（ｘ，ｙ）存在。

３：后接两个整数（ｘ，ｙ），代表将点Ｘ上的权值变成Ｙ。

输入输出格式

输入格式：

第１行两个整数，分别为Ｎ和Ｍ，代表点数和操作数。

第２行到第Ｎ＋１行，每行一个整数，整数在［１，１０＾９］内，代表每个点的权值。

第Ｎ＋２行到第Ｎ＋Ｍ＋１行，每行三个整数，分别代表操作类型和操作所需的量。

输出格式：

对于每一个０号操作，你须输出Ｘ到Ｙ的路径上点权的Ｘｏｒ和。

输入输出样例

输入样例#1：

3 3
1
2
3
1 1 2
0 1 2
0 1 1

输出样例#1：

3
1

说明

数据范围：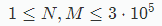 

---

因为只是模板题吧。。在这里直接放上代码。。

关于LCT可以看论文：QTREE解法的一些研究

 #include<cstdio>
 #include<cstring>
 #include<iostream>
 using namespace std;

 int read(){
     char ch;
     int re=;
     bool flag=;
     while((ch=getchar())!='-'&&(ch<''||ch>''));
     ch=='-'?flag=:re=ch-'';
     while((ch=getchar())>=''&&ch<='')  re=re*+ch-'';
     return flag?-re:re;
 }

 struct Splay{
     int ch[],xr,fa;
     bool rev;
 };

 const int maxn=;

 int n,m,top;
 int val[maxn],stk[maxn];
 Splay T[maxn];

 inline void push_up(int x){  T[x].xr=T[T[x].ch[]].xr^T[T[x].ch[]].xr^val[x];   }

 inline bool isroot(int x){
     return T[T[x].fa].ch[]!=x&&T[T[x].fa].ch[]!=x;
 }

 inline void push_down(int x){
     if(T[x].rev){
         T[T[x].ch[]].rev^=;
         T[T[x].ch[]].rev^=;
         swap(T[x].ch[],T[x].ch[]);
         T[x].rev=;
     }
 }

 void rot(int x){
     int y=T[x].fa,z=T[y].fa,l,r;
     if(T[y].ch[]==x)  l=;
     else  l=;
     r=l^;
     T[x].fa=z;
     if(!isroot(y))  T[z].ch[T[z].ch[]==y]=x;
     T[T[x].ch[r]].fa=y;
     T[y].ch[l]=T[x].ch[r];
     T[y].fa=x;
     T[x].ch[r]=y;
     push_up(y),push_up(x);
 }

 void splay(int x){
     top=;  stk[top]=x;
     for(int i=x;!isroot(i);i=T[i].fa)  stk[++top]=T[i].fa;
     for(int i=top;i;i--)  push_down(stk[i]);
     while(!isroot(x)){
         int y=T[x].fa,z=T[y].fa;
         if(!isroot(y)){
             if((T[y].ch[]==x)^(T[z].ch[]==y))  rot(x);
             else  rot(y);
         }
         rot(x);
     }
 }

 void acc(int x){
     int t=;
     while(x){
         splay(x);
         T[x].ch[]=t;
         push_up(x);
         t=x;  x=T[x].fa;
     }
 }

 void make_root(int x){
     acc(x);
     splay(x);
     T[x].rev^=;
 }

 int find(int x){
     acc(x);
     splay(x);
     while(T[x].ch[])  x=T[x].ch[];
     return x;
 }

 void split(int x,int y){
     make_root(x);
     acc(y);
     splay(y);
 }

 void cut(int x,int y){
     split(x,y);
     if(T[y].ch[]==x)  T[y].ch[]=,T[x].fa=;
 }

 void link(int x,int y){
     make_root(x);
     T[x].fa=y;
 }

 int main(){
 //    freopen("temp.in","r",stdin);
     n=read(),m=read();
     for(int i=;i<=n;i++){
         val[i]=read();
         T[i].xr=val[i];
     }
     int opt,x,y,xx,yy;
     while(m--){
         opt=read(),x=read(),y=read();
         switch(opt){
             case :{
                 split(x,y);
                 printf("%d\n",T[y].xr);
                 break;
             }
             case :{
                 xx=find(x),yy=find(y);
                 if(xx!=yy)  link(x,y);
                 break;
             }
             case :{
                 xx=find(x),yy=find(y);
                 if(xx==yy)  cut(x,y);
                 break;
             }
             case :{
                 acc(x);
                 splay(x);
                 val[x]=y;
                 push_up(x);
                 break;
             }
         }
     }
     return ;
 }