[HAOI2015]按位或(容斥+前缀和)

题目描述

刚开始你有一个数字0，每一秒钟你会随机选择一个[0,2^n-1]的数字，与你手上的数字进行或（c++,c的|,pascal

的or）操作。选择数字i的概率是p[i]。保证0<=p[i]<=1，Σp[i]=1问期望多少秒后，你手上的数字变成2^n-1。

题解

MIN-MAX容斥

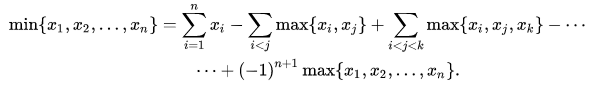
大概就是这么两个东西，做题思路大概就是正难则反吧，max不好求但min好求，就可以直接用这种方法上了。

现在我们算maxV(S)，然鹅它不好算，所以我们就转换求所有minV(S)。

考虑一个事件发生的概率为p，那么我们就有了求min的方法。

sum=1*p+2*(p-1)*p+3*(p-1)^2*p......

然后用高中数学知识，解得它等于1/p。

然后我们的任务变成了求所有子集的p。

这玩意也不太好求，因为所有与这个集合有交的数都会产生贡献。

再次正难则反一下，变成了1-补集，这个补集和很好，它就是补集的高维前缀和。

有人说这是FMT，但好像FWT的异或卷积也长这样？

代码

#include<iostream>
#include<cstdio>
#include<cmath>
#define N (1<<20)+20
using namespace std;
const double eps=1e-;
int n,size,cnt[N];
double ans,a[N];
inline int rd(){
    int x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(f=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
int main(){
    n=rd();size=(<<n);int up=size;
    for(int i=;i<size;++i)scanf("%lf",&a[i]);
    for(int i=;i<size;i<<=)
        for(int j=;j<size;++j)if(!(j&i))a[j|i]+=a[j];
    for(int i=;i<=size;++i)cnt[i]=cnt[i>>]+(i&);
    for(int i=;i<size;++i){
        double x=-a[(size-)^i];
        if(fabs(x)<eps){printf("INF\n");return ;}
        if(cnt[i]&)ans+=(double)/x;else ans-=(double)/x;
    }
    printf("%.10lf",ans);
    return ;
}

我看到网上还有这么一种解法

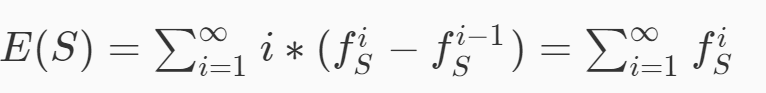
然而我并没有看懂。。。