poj 1733 Parity game（带权并查集+离散化）

题目链接：http://poj.org/problem?id=1733

题目大意：有一个很长很长含有01的字符串，长度可达1000000000，首先告诉你字符串的长度n，再给一个m，表示给你m条信息，接下来的m行每行包含x，y，even/odd，表示区间【x，y】中1的个数，even为偶数，odd为奇数。判断前几条是对的，也就是说假设k+1条信息与前面相互矛盾，就输出k，说明前k条正确。

例：
Sample Input

10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd

Sample Output

3

解题思路：wa了n多次，但是思路正确了，字符串长度太大，开不了那么大的数组，看了题解才知道还可以离散化。

如果不会离散化，就看下这个博客：https://blog.csdn.net/xiangaccepted/article/details/73276826

不过我没有用那里的方法离散化，直接看大佬的，用map离散化挺方便的，因为这些数本身大小不重要，而重要的是他们的相对关系，所以可以进行离散化处理。

做法就是运用带权并查集，区间【x，y】中1的个数为偶数时，说明前x-1个数和前y个数中1的个数奇偶性相同，反之区间【x，y】1的个数为奇数，说明前x-1个数和前y个数中1的个数奇偶性不同。我们就可以用一个关系数组relation【】存储该节点与其父亲节点的奇偶性是否一致（0相同，1不相同）。

然后问题就在于更新它们的关系域了

第一个是查找的时候，还要进行路径压缩，所以节点的关系域要更新。

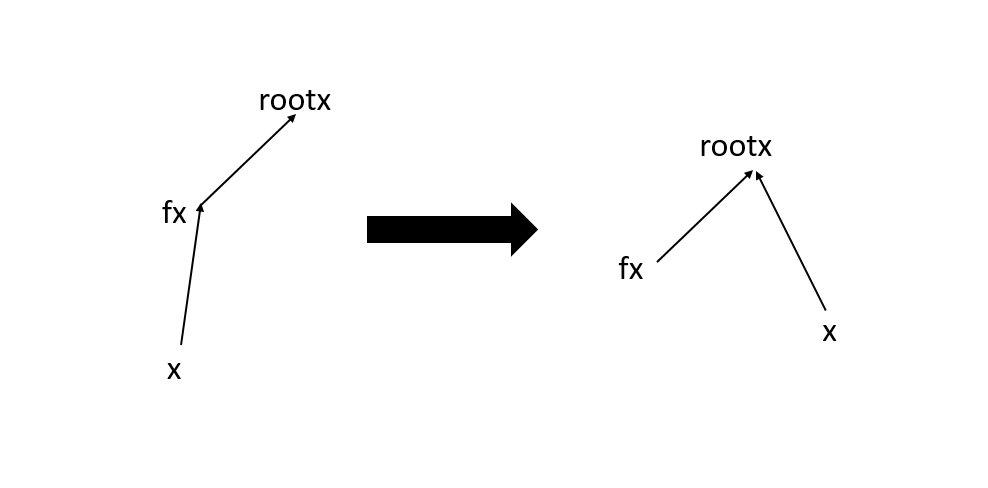
假设做图是路径压缩前，右图是路径压缩后，我们把可以简单的对他们的关系进行枚举，就可以找到他们的关系了

relation【x】　　relation【fx】　　更新后relation【x】

0　　0　　0

0　　1　　1

1　　0　　1

1　　1　　0

很明显就是异或的关系，所以可以得到relation[x]=(relation[x]+relation[par[x]])%2，也就是relation[x]=relation[x]^relation[par[x]].

还有就是当两个元素的根不一样时需要合并两个集合，假如是将x所在集合的根rootx合并到y所在的集合的根rooty，这时候rootx的关系域也要进行更新，因为原本它的父亲节点是它自己，后来变成了rooty。

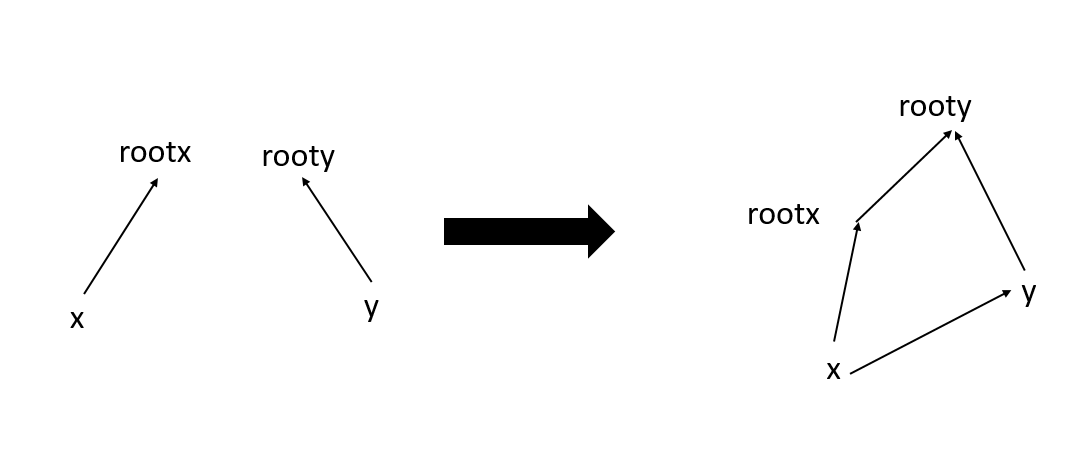
从左图变成右图，再作了一条辅助线，x->y便于理解下，我们要求的更新后relation【rootx】与它的父亲节点rooty的关系

看到这图我们是不是可以想想可不可以用向量去做呢？事实证明是可以的

根据向量的知识我们可以知道：rootx->rooy=x->y+y->rooty-x->rootx

这不就等价于我们的：relation[rootx]=x与y的关系d+relation[y]-relation[x]

为了保证不超出我们的关系的范围（【0，1】）所以我们的式子为relation[fx]=(d+relation[y]-relation[x]+2)%2（加2保证结果不为负数）

还有最后一个就是当x和y的根节点已经相同时，我们怎么判断是否与前面的信息有矛盾呢？

其实就是我们查找时更新关系域是一样的。

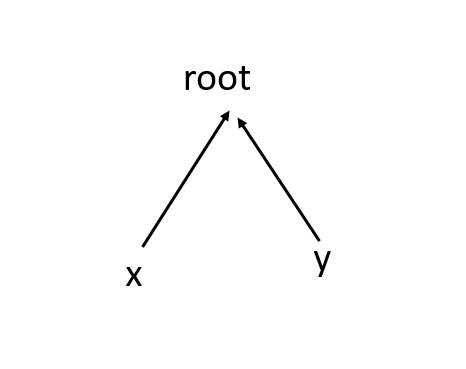
relation【x】　　relation【y】　　d（x与y的关系）

0　　0　　0

0　　1　　1

1　　0　　1

1　　1　　0

直接判断relation[x]^relation[y]==d

如果不等于肯定是有矛盾的。

思路基本就这样，其他也没什么了，看代码吧。

这应该是我写的最详细的一篇解题报告了。。。

附上代码：

 #include<iostream>
 #include<cstdio>
 #include<map>
 #include<cstring>
 using namespace std;
 int par[*],relation[*];
 int ans,q;

 void init(int x)
 {
     for(int i=;i<=x;i++)
     {
         par[i]=i;
         relation[i]=;
     }
 }

 int find(int x)
 {
     if(x!=par[x])
     {
         int temp=find(par[x]);
         relation[x]=(relation[x]+relation[par[x]])%;  //更新relation[x]
         par[x]=temp;
     }
     return par[x];
 }

 void unite(int x,int y,int d,int cnt)  //d是x和y的关系，cnt是第几条消息
 {
     int fx=find(x);
     int fy=find(y);
     if(fx==fy)
     {
         if(relation[x]^relation[y]!=d&&q==)
         {
             ans=cnt-;  //第cnt条消息矛盾，说明前cnt-1条消息对的
             q++;
         }
         return;
     }
     else
     {
         par[fx]=fy;
         relation[fx]=(d+relation[y]-relation[x]+)%;
     }
 }

 bool same(int x,int y)
 {
     return find(x)==find(y);
 }

 signed main()
 {
     int n,m;
     map<int,int> mp;  //用于离散化
     while(cin>>n>>m)
     {
         mp.clear();
         init(*);
         ans=m;
         int count=;
         int k=,q=;
         while(m--)
         {
             int a,b,d;
             char s[];
             cin>>a>>b>>s;
             if(!mp[a-])
                 mp[a-]=count++;
             if(!mp[b])
                 mp[b]=count++;
             if(s[]=='e') d=;  //偶数，x-1和y奇偶性相同
             else d=;
             unite(mp[a-],mp[b],d,k);  //k是记录第几条消息
             k++;
         }
         cout<<ans<<endl;
     }
     return ;
 }