洛谷mNOIP模拟赛Day2-入阵曲

题目背景

pdf题面和大样例链接：http://pan.baidu.com/s/1cawM7c 密码：xgxv

丹青千秋酿，一醉解愁肠。
无悔少年枉，只愿壮志狂。 

题目描述

小 F 很喜欢数学，但是到了高中以后数学总是考不好。

有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的 时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以 解决的问题，被一个又一个算法轻松解决。

小 F 当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。

一年过去了，想想都还有点恍惚。

他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不 已。也许，这就是热血吧。

也就是在那个时候，小 F 学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的 第 10^{100}10100 项，真是奇妙无比呢。

不过，小 F 现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小 问题。他写写画画，画出了一个 n \times mn×m 的矩阵，每个格子里都有一个不超过 kk 的正整数。

小 F 想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是 kk 的倍数？ 如果把一个子矩形用它的左上角和右下角描述为 (x_1,y_1,x_2,y_2)(x1​,y1​,x2​,y2​)，其中x_1 \le x_2,y_1 \le y_2x1​≤x2​,y1​≤y2​； 那么，我们认为两个子矩形是不同的，当且仅当他们以 (x_1,y_1,x_2,y_2)(x1​,y1​,x2​,y2​) 表示时不同；也就是 说，只要两个矩形以 (x_1,y_1,x_2,y_2)(x1​,y1​,x2​,y2​) 表示时相同，就认为这两个矩形是同一个矩形，你应该 在你的答案里只算一次。

输入输出格式

输入格式：

从标准输入中读入数据。

输入第一行，包含三个正整数 n,m,kn,m,k。

输入接下来 nn 行，每行包含 mm 个正整数，第 ii 行第 jj 列表示矩阵中第 ii 行第 jj 列 中所填的正整数 a_{i,j}ai,j​。

输出格式：

输出到标准输出中。

输入一行一个非负整数，表示你的答案。

输入输出样例

输入样例#1： 复制

2 3 2
1 2 1
2 1 2

输出样例#1： 复制

6

说明

【样例 1 说明】

这些矩形是符合要求的： (1, 1, 1, 3)，(1, 1, 2, 2)，(1, 2, 1, 2)，(1, 2, 2, 3)，(2, 1, 2, 1)，(2, 3, 2, 3)。

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解 决一部分测试数据。

每个测试点的数据规模及特点如下表：

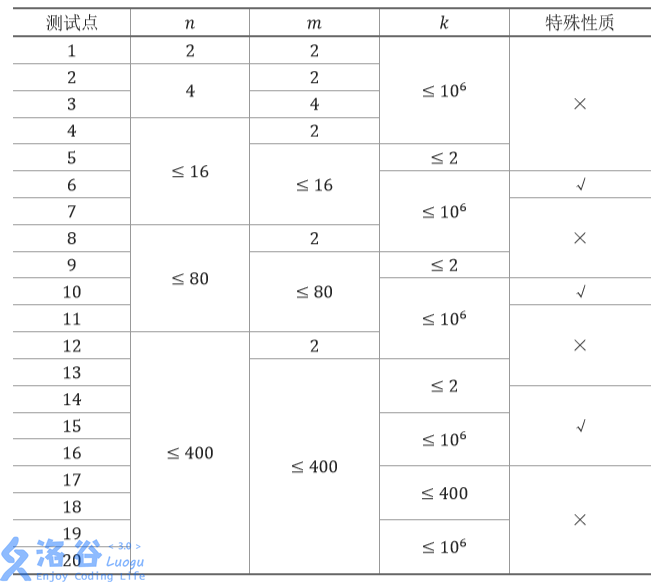
特殊性质：保证所有ai,j​ 均相同。

---

暴力的话枚举就是了，预处理一下sum

同时所有a相同的情况可以骗到5分

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<cmath>
 #include<map>
 #include<set>
 #include<queue>
 #include<vector>
 #define INF 0x7f7f7f7f
 #define pii pair<int,int>
 #define ll long long
 using namespace std;
 int n,m,k;
 int a[][];
 namespace solve1
 {
     int n,m,k;
     ll s[][];
     int a[][];
     void solve(){
         n=::n,m=::m,k=::k;
         memcpy(a,::a,sizeof(a));
         for(int i=;i<=n;i++){
             for(int j=;j<=m;j++){
                 s[i][j]=s[i-][j]+s[i][j-]-s[i-][j-]+a[i][j];
             }
         }
         ll ans=;
         for(int i=;i<=n;i++){
             for(int j=;j<=m;j++){
                 for(int x=i;x<=n;x++){
                     for(int y=j;y<=m;y++){
                         if(!((s[x][y]-s[i-][y]-s[x][j-]+s[i-][j-])%k)){
                             ans++;
                         }
                     }
                 }
             }
         }
         printf("%lld\n",ans);
     }
 }
 namespace solve2
 {
     int n,m,k;
     int K;
     int a[][];
     int gcd(int x,int y){
         return (y==?x:gcd(y,x%y));
     }
     void solve(){
         n=::n,m=::m,k=::k;
         memcpy(a,::a,sizeof(a));
         int g=gcd(a[][],k);
         K=k/g;
         ll ans=;
         for(int i=;i*K<=n*m;i++){
             int t=i*K;
             for(int j=;j<=t;j++){
                 if(t%j==){
                     int x=j,y=t/j;
                     if(x<=n&&y<=m){
                         ans+=(n-x+)*(m-y+);
                     }
                 }
             }
         }
         printf("%lld\n",ans);
     }
 }
 int read(){
     int x=,f=;char ch=getchar();
     while(ch<''||ch>''){if('-'==ch)f=-;ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x*f;
 }
 int main()
 {
 //    freopen("rally1.in","r",stdin);
     n=read(),m=read(),k=read();
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             a[i][j]=read();
         }
     }
     int t=a[][],ok=;
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(t!=a[i][j]){
                 ok=;
                 break;
             }
         }
         if(!ok){
             break;
         }
     }
     if(ok){
         solve2::solve();
     }
     else{
         solve1::solve();
     }
     return ;
 }

暴力

我们发现无法遍历所有的矩阵，一旦遍历就会超时

于是只能用一些鬼畜的计数方法，然而并不是很好发现

只好去一维看看：

给定一个序列，求连续的子序列之和是k的倍数的数目

然后我们鬼畜地想到了前缀和：如果两个前缀和模k相同，那么这两个前缀和之差对应的区间一定是k的倍数

这样就有了思路，统计所有前缀和模k的情况，然后对于模k结果相同的前缀，任选两个相减对应的区间一定是k的倍数

注意如果前缀和本身就是k的倍数，可以看成它和前零个数的前缀和构成k倍数的区间，所以把0的位置+1即可

这样的复杂度是O(n)

回到二维的情况：

发现问题迎刃而解，枚举压起来然后就是上面的问题了

O(n^3)

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 #include<cstring>
 #include<vector>
 #define MAXN 405
 #define ll long long
 using namespace std;
 int read(){
     int x=;char ch=getchar();
     while(ch<''||ch>''){ch=getchar();}
     while(ch>=''&&ch<=''){x=x*+ch-'';ch=getchar();}
     return x;
 }
 ll ans;
 int n,m,k;
 int a[MAXN][MAXN];
 ll s[MAXN][MAXN];
 ll b[MAXN];
 int t[];
 int vis[],cnt;
 void work(int x,int y){
     cnt++;
     vector<int> v;
     for(int i=;i<=m;i++){
         b[i]=s[i][y]-s[i][x-];
     }
     t[]=;
     vis[]=cnt;
     v.push_back();
     for(int i=;i<=m;i++){
         b[i]+=b[i-];
         int p=b[i]%k;
         if(vis[p]!=cnt){
             vis[p]=cnt;
             t[p]=;
             v.push_back(p);
         }
         t[p]++;
     }
     for(int i=;i<v.size();i++){
         int x=v[i];
         ans+=1LL*t[x]*(t[x]-)/;
     }
 }
 int main()
 {
     n=read(),m=read(),k=read();
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             a[i][j]=read();
         }
     }
     for(int j=;j<=m;j++){
         for(int i=;i<=n;i++){
             s[j][i]=s[j][i-]+a[i][j];
         }
     }
     for(int i=;i<=n;i++){
         for(int j=i;j<=n;j++){
             work(i,j);
         }
     }
     printf("%lld\n",ans);
     return ;
 }

AC

总结：二维可以拿一维的思想来考虑，当枚举不能解决问题时肯定有计数的策略