正则化（Regularization）本质

参考：

http://www.cnblogs.com/maybe2030/p/9231231.html

https://blog.csdn.net/wsj998689aa/article/details/39547771

https://charlesliuyx.github.io/2017/10/03/%E3%80%90%E7%9B%B4%E8%A7%82%E8%AF%A6%E8%A7%A3%E3%80%91%E4%BB%80%E4%B9%88%E6%98%AF%E6%AD%A3%E5%88%99%E5%8C%96/

1、正则化是什么

正则化看起来有些抽象，其直译"规则化"，本质其实很简单，就是给模型加一些规则限制，约束要优化参数，目的是防止过拟合。其中最常见的规则限制就是添加先验约束，其中L1相当于添加Laplace先验，L相当于添加Gaussian先验。

2、L1正则和L2正则

L1正则是在原始的loss函数上加上一个L1正则化项，这个L1正则项实际就是在loss函数上添加一个结构化风险项，因此正则化其实和“带约束的目标函数”是等价的。而L1正则项就是一个1范数，本质相当于添加一个Laplace先验知识。同理，L2正则化项是一个2范数，本质却相当于添加一个Gaussian先验知识。

参考http://www.cnblogs.com/heguanyou/p/7582578.html。

3、范数

参考：https://charlesliuyx.github.io/2017/10/03/%E3%80%90%E7%9B%B4%E8%A7%82%E8%AF%A6%E8%A7%A3%E3%80%91%E4%BB%80%E4%B9%88%E6%98%AF%E6%AD%A3%E5%88%99%E5%8C%96/

我们知道，范数（norm）的概念来源于泛函分析与测度理论，wiki中的定义相当简单明了：范数是具有“长度”概念的函数，用于衡量一个矢量的大小（测量矢量的测度）

我们常说测度测度，测量长度，也就是为了表征这个长度。而如何表达“长度”这个概念也是不同的，也就对应了不同的范数，本质上说，还是观察问题的方式和角度不同，比如那个经典问题，为什么矩形的面积是长乘以宽？这背后的关键是欧式空间的平移不变性，换句话说，就是面积和长成正比，所以才有这个

没有测度论就没有（现代）概率论。而概率论也是整个机器学习学科的基石之一。测度就像尺子，由于测量对象不同，我们需要直尺量布匹、皮尺量身披、卷尺量房间、游标卡尺量工件等等。注意，“尺子”与刻度（寸、米等）是两回事，不能混淆。

范数分为向量范数（二维坐标系）和矩阵范数（多维空间，一般化表达），如果不希望太数学化的解释，那么可以直观的理解为：0-范数：向量中非零元素的数量；1-范数：向量的元素的绝对值；2-范数：是通常意义上的模（距离）

范数的图形表示如下：

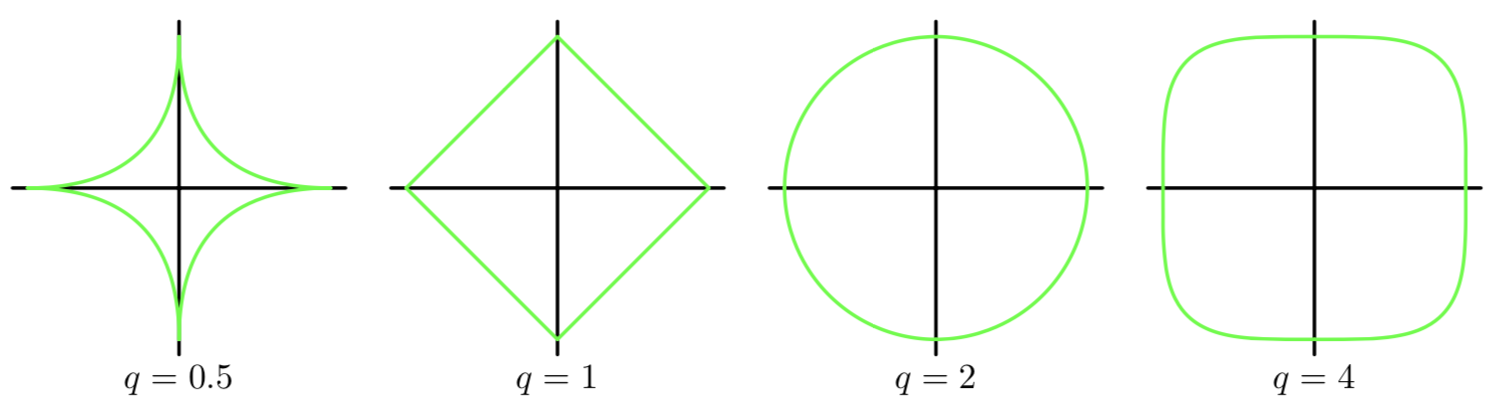
4、正则化为什么就能防止过拟合

参考：http://www.cnblogs.com/heguanyou/p/7582578.html

过拟合的时候，拟合函数的系数往往非常大，为什么？如下图所示，过拟合，就是拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大。在某些很小的区间里，函数值的变化很剧烈。这就意味着函数在某些小区间里的导数值（绝对值）非常大，由于自变量值可大可小，所以只有系数足够大，才能保证导数值很大。

从几何解释：

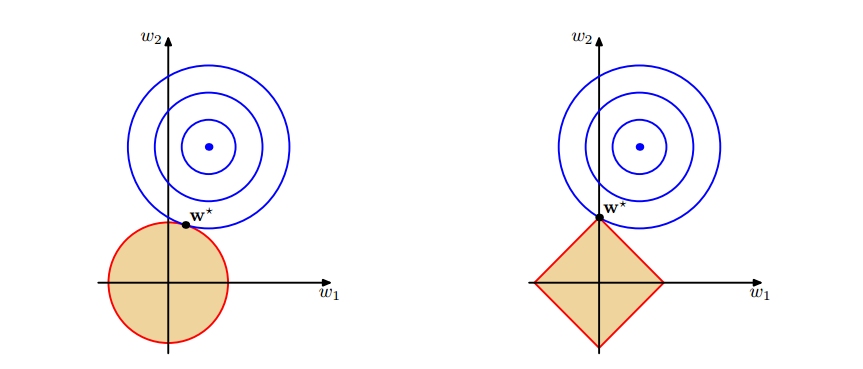
图1 上面中的蓝色轮廓线是没有正则化损失函数的等高线，中心的蓝色点为最优解，左图、右图分别为L2、L1正则化给出的限制。

可以看到在正则化的限制之下，L2正则化给出的最优解 $w^{*} $是使解更加靠近原点，也就是说L2正则化能降低参数范数的总和，使得模型的解偏向于 norm 较小的 W，通过限制 W 的 norm 的大小实现了对模型空间的限制，从而在一定程度上避免了 overfitting 。不过 L2正则化并不具有产生稀疏解的能力，得到的系数 仍然需要数据中的所有特征才能计算预测结果，从计算量上来说并没有得到改观。

L1正则化给出的最优解$w^{*}$是使解更加靠近某些轴，而其它的轴则为0，所以L1正则化能使得到的参数稀疏化。稀疏的解除了计算量上的好处之外，更重要的是更具有“可解释性”。比如说，一个病如果依赖于 5 个变量的话，将会更易于医生理解、描述和总结规律，但是如果依赖于 5000 个变量的话，基本上就超出人肉可处理的范围了。

因此正则化是通过约束参数的范数使其不要太大，使其在一定程度上减少过拟合情况。

5、Dropout与Batch Normalization

http://www.cnblogs.com/maybe2030/p/9231231.html