AtCoder ABC 042D いろはちゃんとマス目 / Iroha and a Grid

题目链接：https://abc042.contest.atcoder.jp/tasks/arc058_b

题目大意：

　　给定一个 H * W 的矩阵，其中左下角 A * B 区域是禁区，要求在不踏入禁区的前提下，从左上角走到右下角一共有多少种走法？

分析：

　　设 D 为往下，R为往左。

这里举个 H = 10，W = 7，A = 3，B = 4的例子：

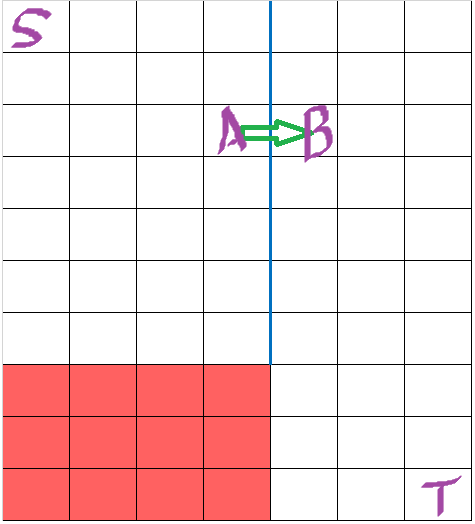
首先不管怎么走，路线都是要跨越蓝色边界线的，这里我们只讨论从 A 跨越到 B 的情况，其余情况同理。

在这种情况下，总的路数就是所有从 S 走到 A 的路线总数乘上所有从 B 走到 T 的路线总数。

从 S 走到 A 的路线总数就是组合数 C(5, 2)，这是因为从 S 走到 A 需要走2个 D 和3个 R，也就是说，2个 D 和3个 L 能组合出多少不同的序列，这是非常基本的组合题，答案就是5个里选2个即 C(5, 2)。

同理从 B 走到 T 的路线总数为 C(9, 2)。

于是这种情况下的总路数为 C(5, 2) * C(9, 2)。

找一下规律把所有情况加起来即可，注意数据规模很大，所以在求组合数时要用到逆元。

代码如下：

 #pragma GCC optimize("Ofast")
 #include <bits/stdc++.h>
 using namespace std;

 #define INIT() std::ios::sync_with_stdio(false);std::cin.tie(0);
 #define Rep(i,n) for (int i = 0; i < (n); ++i)
 #define For(i,s,t) for (int i = (s); i <= (t); ++i)
 #define rFor(i,t,s) for (int i = (t); i >= (s); --i)
 #define ForLL(i, s, t) for (LL i = LL(s); i <= LL(t); ++i)
 #define rForLL(i, t, s) for (LL i = LL(t); i >= LL(s); --i)
 #define foreach(i,c) for (__typeof(c.begin()) i = c.begin(); i != c.end(); ++i)
 #define rforeach(i,c) for (__typeof(c.rbegin()) i = c.rbegin(); i != c.rend(); ++i)

 #define pr(x) cout << #x << " = " << x << "  "
 #define prln(x) cout << #x << " = " << x << endl

 #define LOWBIT(x) ((x)&(-x))

 #define ALL(x) x.begin(),x.end()
 #define INS(x) inserter(x,x.begin())

 #define ms0(a) memset(a,0,sizeof(a))
 #define msI(a) memset(a,inf,sizeof(a))
 #define msM(a) memset(a,-1,sizeof(a))

 #define MP make_pair
 #define PB push_back
 #define ft first
 #define sd second

 template<typename T1, typename T2>
 istream &operator>>(istream &in, pair<T1, T2> &p) {
     in >> p.first >> p.second;
     return in;
 }

 template<typename T>
 istream &operator>>(istream &in, vector<T> &v) {
     for (auto &x: v)
         in >> x;
     return in;
 }

 template<typename T1, typename T2>
 ostream &operator<<(ostream &out, const std::pair<T1, T2> &p) {
     out << "[" << p.first << ", " << p.second << "]" << "\n";
     return out;
 }

 typedef long long LL;
 typedef unsigned long long uLL;
 typedef pair< double, double > PDD;
 typedef pair< int, int > PII;
 typedef set< int > SI;
 typedef vector< int > VI;
 typedef map< int, int > MII;
 const double EPS = 1e-;
 const int inf = 1e9 + ;
 const LL mod = 1e9 + ;
 const int maxN = 1e5 + ;
 const LL ONE = ;
 const LL evenBits = 0xaaaaaaaaaaaaaaaa;
 const LL oddBits = 0x5555555555555555;

 LL fac[ * maxN];
 void init_fact() {
     fac[] = ;
     For(i, ,  * maxN - ) {
         fac[i] = (i * fac[i - ]) % mod;
     }
 }

 //ax + by = gcd(a, b) = d
 // 扩展欧几里德算法
 inline void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){
     if (!b) {d = a, x = , y = ;}
     else{
         ex_gcd(b, a % b, y, x, d);
         y -= x * (a / b);
     }
 }

 // 求a关于p的逆元，如果不存在，返回-1
 // a与p互质，逆元才存在
 inline LL inv_mod(LL a, LL p){
     LL d, x, y;
     ex_gcd(a, p, x, y, d);
     return d ==  ? (x % p + p) % p : -;
 }

 // Calculate x^y % p
 inline LL pow_mod(LL x, LL y, LL p){
     LL ans = ;
     while(y){
         if(y & ) ans = (ans * x) % p;
         x = (x * x) % p;
         y >>= ;
     }
     return ans;
 } 

 inline LL comb_mod(LL m,LL n){
     LL ans;
     if(m > n) swap(m, n);

     ans = (fac[n] * inv_mod(fac[m], mod)) % mod;
     ans = (ans * inv_mod(fac[n - m], mod)) % mod;

     return ans;
 }

 int H, W, A, B;
 LL ans;

 int main(){
     INIT();
     init_fact();
     cin >> H >> W >> A >> B;
     For(i, , H - A) {
         ans += (comb_mod(i - , i + B - ) * comb_mod(W - B - , W - B + H - i - )) % mod;
         ans %= mod;
     }

     cout << ans << endl;
     return ;
 }