Probability&Statistics 概率论与数理统计(1)

基本概念

样本空间: 随机试验E的所有可能结果组成的集合, 为E的样本空间, 记为S

随机事件: E的样本空间S的子集为E的随机事件, 简称事件, 由一个样本点组成的单点集, 称为基本事件

对立事件/逆事件: 若A并B=S, 且A交B=空, 则称A与B互为逆事件, A与B互为对立事件. A上面加一横即A的逆事件

频率: 在相同的条件下进行了n次试验, 事件A发生的次数为A的频数, 与n的比值成为A的频率

概率: 设E为随机试验, S是E的样本空间, 对于E的每一个事件A赋予一个实数, 记为P(A), 称为A的概率, 用于表征事件A在一次试验中发生的可能性的大小

条件概率

基本公式: 设A, B是两个事件, 且P(A) > 0, 称 P(B|A) = P(AB) / P(A) 为在事件A发生的条件下事件B发生的条件概率

乘法定理: 设 P(A) > 0, 则有 P(AB) = P(B|A) * P(A), 以及 P(ABC) = P(C|AB) * P(B|A) * P(A)

全概率公式: 设试验E的样本空间为S, A为E的事件, B₁, B₂, ..., B_n为S的一个划分, 且P(B_i) > 0, 则
P(A) = P(A|B₁) * P(B₁) + P(A|B₂) * P(B₂) + ... + P(A|B_n) * P(B_n)
实际问题中, P(A)不容易直接求得, 可以通过容易求得的P(A|B_i) * P(B_i)间接求得.

贝叶斯公式: 设试验E的样本空间为S, A为E的事件, B₁, B₂, ..., B_n为S的一个划分, 且P(A) > 0, P(B_i) > 0, 则
P(B_i|A) = P(A|B_i) * P(B_i) / (∑ P(A|B_j) * P(B_j))

全概率公式和贝叶斯公式在n = 2的情况下的相同形式

P(B|A) = P(A|B) * P(B) / (P(A|B) * P(B) + P(A|B^) * P(B^))

随机变量及其分布

当样本空间S的元素不是一个数时, 对于S就难以描述和研究. 将随机试验的每一个结果, 即将S的每个元素e与实数x对应起来, 从而引入随机变量的概念. 用e代表样本空间的元素, 将样本空间记为{e}

随机变量: 设随机试验的样本空间为S = {e}, X = X(e) 是定义在样本空间S上的实值单值函数. 称X = X(e) 为随机变量

离散型随机变量

定义: 有些随机变量, 全部可能取到的值是有限个或可列无限多个, 这种随机变量称为离散型随机变量.

离散型随机变量分布

(0-1)分布: 设随机变量X只可能取0与1两个值, 它的分布律是 P{ X = k } = p^k * (1 - p)^{1 - k}, k = 0, 1 (0 < p < 1) 则称X服从以p为参数的(0 - 1) 分布或两点分布

Bernoulli experiment 伯努利试验: 设试验E只有两个可能结果, A及A^, 则称E为伯努利试验.  这是在同样的条件下重复地、相互独立地进行的一种随机试验，其特点是该随机试验只有两种可能结果：发生或者不发生。我们假设该项试验独立重复地进行了n次，那么就称这一系列重复独立的随机试验为n重伯努利试验，或称为伯努利概型。单个伯努利试验是没有多大意义的，然而，当我们反复进行伯努利试验，去观察这些试验有多少是成功的，多少是失败的，事情就变得有意义了

二项分布: 以X表示n重伯努利试验中A发生的次数, X是一个随机变量, 可能取值为0 ~ n, 事件A在指定的k次试验中发生, 在其他 n - k 次试验中不发生的概率为 p^k * (1 - p)^{n - k}. 这种制定的方式共有C_kⁿ种, 故在n次试验中A发生k次的概率为P{ X = k } = C_kⁿ * p^k * (1 - p)^{n - k}. 称随机变量X服从参数为n, p的二项分布, 并记为X ~ b(n, p)

泊松分布: 设随机变量X所有可能取的值为0, 1, 2, ..., 而取各个值的概率为
P{ X = k } = λ^k * e^-λ / k! , k = 0, 1, 2, ... 其中λ > 0是常数, 则称X服从参数为λ的泊松分布, 记为 X ~ π(λ)
其中λ = n * p, 泊松分布适用于计算n很大而p很小的情况(n > 20, p < 0.05)

例如: 次品率为0.1%的1000只产品中至少有2个次品的概率, 以X记产品中的次品数, X ~ b(1000, 0.001)
解: λ = n * p = 1000 * 0.001 = 1, P{ X >= 2 } = 1 - P{ X = 0 } - P{ X = 1 } = 1 - e^-1 - e^-1 ≈ 0.2642411

随机变量的分布函数

对于非离散型随机变量X, 由于其可能的取值不能一一列举, 因而不能像离散型随机变量那样可以用分布律来描述它, 另外通常遇到的非离散型随机变量取任一指定的实数值的概率都等于0. 再者, 对于非离散型随机变量, 我们不会对具体某个值的概率感兴趣, 而是对某个区间的概率感兴趣. 因而我们会研究值落在某一个区间(x₁, x₂]的概率P{ x₁ < X <= x₂ }.

随机变量分布函数:
设X是一个随机变量, x是任意实数, 函数 F(x) = P{ X <= r}, -∞<r<∞ 称为X的分布函数
对于任意实数x₁, x₂ (x₁ < x₂), 有 P{ x₁ < X <= x₂ } = P{ X <= x₂ } - P{ X <= x₁ } = F(x₂) - F(x₁)
因此, 若已知X的分布函数, 就知道X在任一区间的概率. 从这个意义上说分布函数完整地描述了随机变量的统计规律性.

连续型随机变量及其概率密度

如果对于随机变量X的分布函数F(x), 存在非负函数f(x), 使得对于任意实数x, F(x)为f(t)对-∞ < t < x的积分, 则称X为连续型随机变量, 其中f(x)称为X的概率密度函数, 简称概率密度

注意: 对于连续型随机变量X, 它取任一指定的实数值a的概率均为0, 及P{ X = a } = 0, 但这不意味着a为不可能事件.

三种重要的连续型随机变量:

均匀分布: 在区间(a, b)里, 概率密度均匀分布 f(x) = 1 / (b - a)

指数分布: 在x > 0时, f(x) =  e^-x/θ / θ
对于服从指数分布的随机变量X, 有如下性质: P{ X > s + t | X > s } = P{ X > t }, 称为无记忆性.

正态分布, 高斯分布:

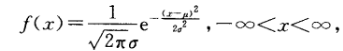
其中μ, σ(σ > 0)为常数, 一般使用均值作为μ, 标准差(Standard Deviation [ˌdi:viˈeɪʃn] )作为σ, 称X服从参数为μ, σ的正态分布或高斯Gauss分布, 记为 X ~ N(μ, σ²)

特点:
1. 曲线关于x = μ 对称
2.当x = μ 时f(x)取到最大值
3. 在x = μ ± σ处曲线有拐点, μ ± σ 的区间占到所有样本的68.2%,  μ ± 2σ 的区间占到95.44%
4. 尽管正态分布的取值范围是(-∞, ∞), 但是值落在(μ - 3σ, μ + 3σ)是大概率事件(99.72%), 这就是3σ法则.

在自然现象和社会现象中, 大量随机变量都服从或近似服从正态分布, 例如身高, 测量误差, 热噪声等.

随机变量的函数的分布

在实际应用中, 一些随机变量不能直接测量, 但是它是某个能直接测量的随机变量的函数. 例如能测量信号响应的时间, 而关心的是距离; 能测量的是电压v, 而关心的是光照强度D. 这里随机变量D是v的函数. 需要通过已知的随机变量X的概率分布去计算它的函数Y=g(X)的概率分布.