深度学习面试题03：改进版梯度下降法Adagrad、RMSprop、Momentum、Adam

目录

　　Adagrad法

　　RMSprop法

　　Momentum法

　　Adam法

　　参考资料

---

发展历史

标准梯度下降法的缺陷

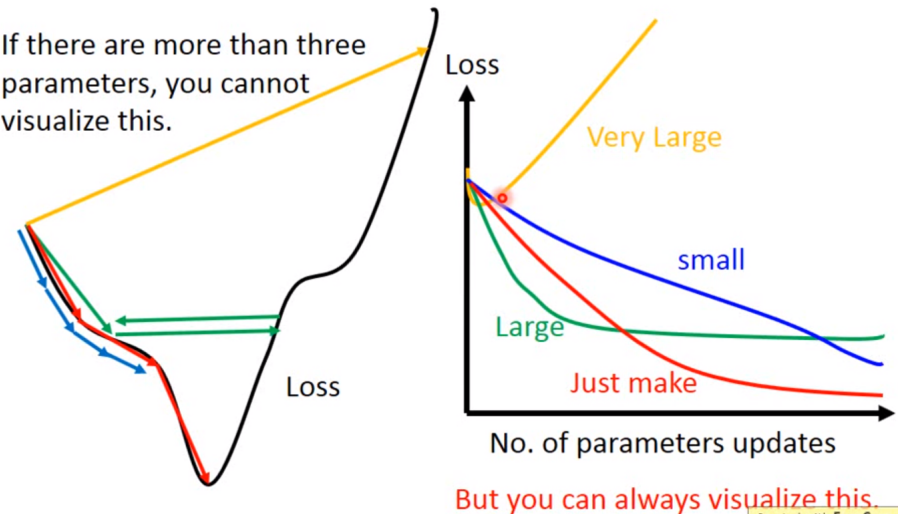
如果学习率选的不恰当会出现以上情况

因此有一些自动调学习率的方法。一般来说，随着迭代次数的增加，学习率应该越来越小，因为迭代次数增加后，得到的解应该比较靠近最优解，所以要缩小步长η，那么有什么公式吗？比如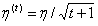：，但是这样做后，所有参数更新时仍都采用同一个学习率，即学习率不能适应所有的参数更新。

解决方案是：给不同的参数不同的学习率

Adagrad法

假设N元函数f(x)，针对一个自变量研究Adagrad梯度下降的迭代过程，

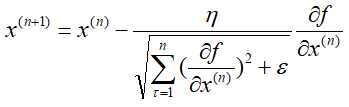
可以看出，Adagrad算法中有自适应调整梯度的意味（adaptive gradient），学习率需要除以一个东西，这个东西就是前n次迭代过程中偏导数的平方和再加一个常量最后开根号。

举例：使用Adagrad算法求y = x²的最小值点

导函数为g(x) = 2x

初始化x⁽⁰⁾ = 4，学习率η=0.25，ε=0.1

第①次迭代：

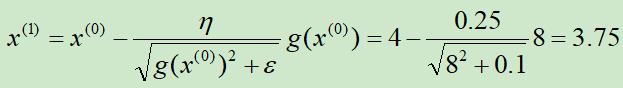
第②次迭代：

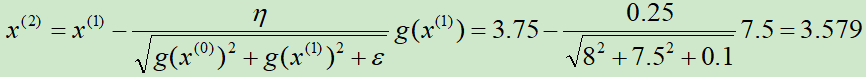
第③次迭代：

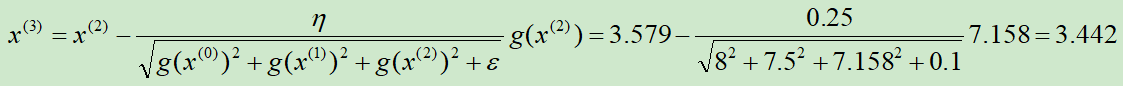
求解的过程如下图所示

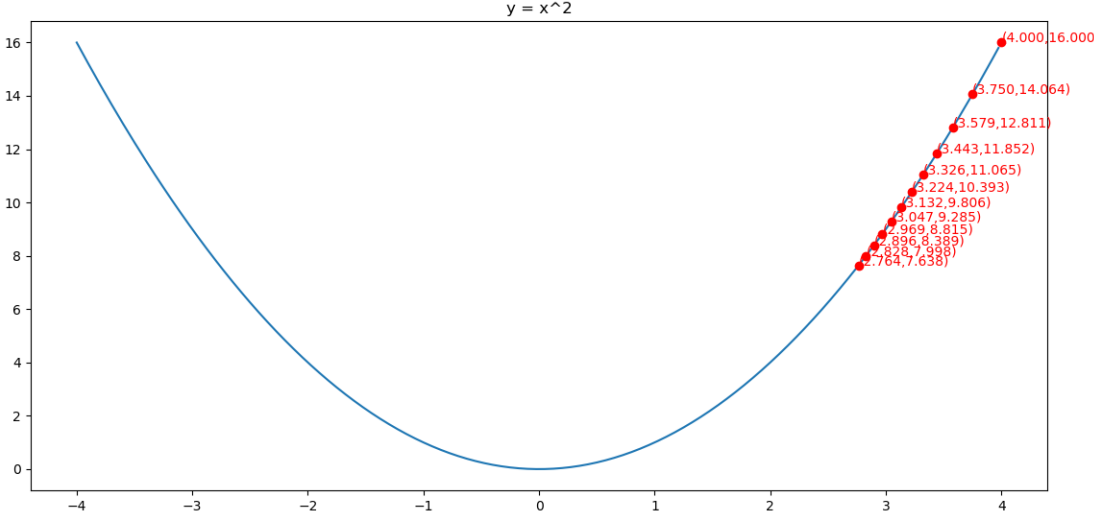
对应代码为：

缺点：由于分母是累加梯度的平方，到后面累加的比较大时，会导致梯度更新缓慢

返回目录

RMSprop法

AdaGrad算法在迭代后期由于学习率过小，可能较难找到一个有用的解。为了解决这一问题，RMSprop算法对Adagrad算法做了一点小小的修改，RMSprop使用指数衰减只保留过去给定窗口大小的梯度，使其能够在找到凸碗状结构后快速收敛。

假设N元函数f(x)，针对一个自变量研究RMSprop梯度下降的迭代过程，

可以看出分母不再是一味的增加，它会重点考虑距离他较近的梯度（指数衰减的效果），也就不会出现Adagrad到后期收敛缓慢的问题

举例：使用RMSprop算法求y = x²的最小值点

导函数为h(x) = 2x

初始化g⁽⁰⁾ = 1，x⁽⁰⁾ = 4，ρ=0.9，η=0.01，ε=10^-10

第①次迭代：

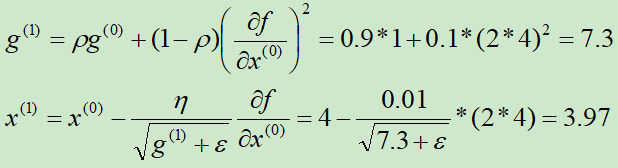
第②次迭代：

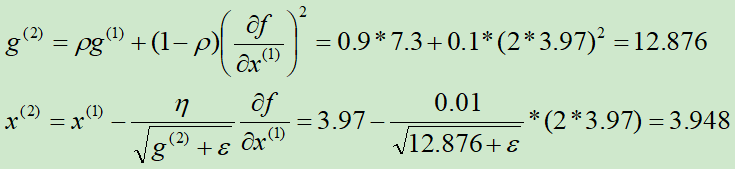
求解的过程如下图所示

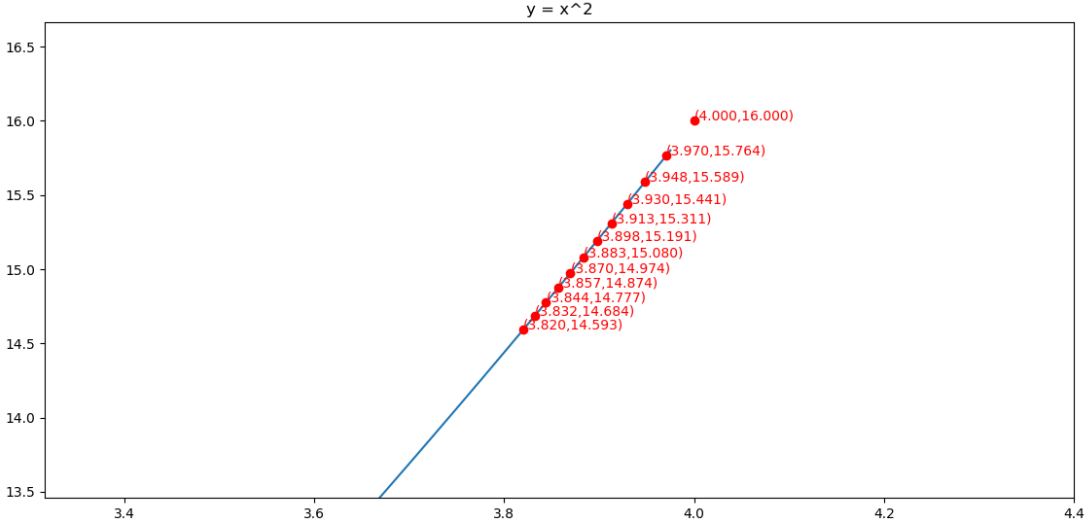
对应代码为：

返回目录

Momentum法

Momentum是动量的意思，想象一下，一个小车从高坡上冲下来，他不会停在最低点，因为他还有一个动量，还会向前冲，甚至可以冲过一些小的山丘，如果面对的是较大的坡，他可能爬不上去，最终又会倒车回来，折叠几次，停在谷底。

如果使用的是没有动量的梯度下降法，则可能会停到第一个次优解

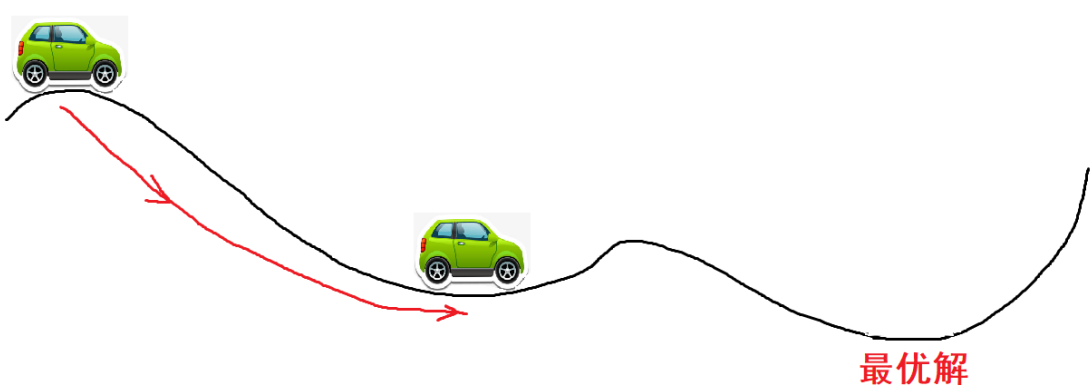
最直观的理解就是，若当前的梯度方向与累积的历史梯度方向一致，则当前的梯度会被加强，从而这一步下降的幅度更大。若当前的梯度方向与累积的梯度方向不一致，则会减弱当前下降的梯度幅度。

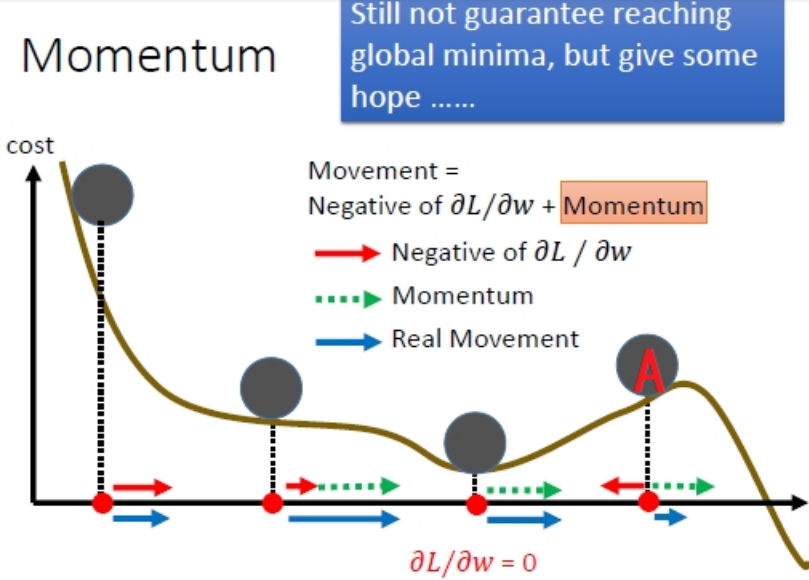
从这幅图可以看出来，当小球到达A点处，负梯度方向的红箭头朝着x轴负向，但是动量方向（绿箭头）朝着x轴的正向并且长度大于红箭头，因此小球在A处还会朝着x轴正向移动。

下面正式介绍Momentum法

假设N元函数f(x)，针对一个自变量研究Momentum梯度下降的迭代过程，

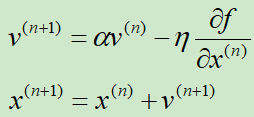
v表示动量，初始v=0

α是一个接近于1的数，一般设置为0.9，也就是把之前的动量缩减到0.9倍

η是学习率

下面通过一个例子演示一下，求y = 2*x^4-x^3-x^2的极小值点

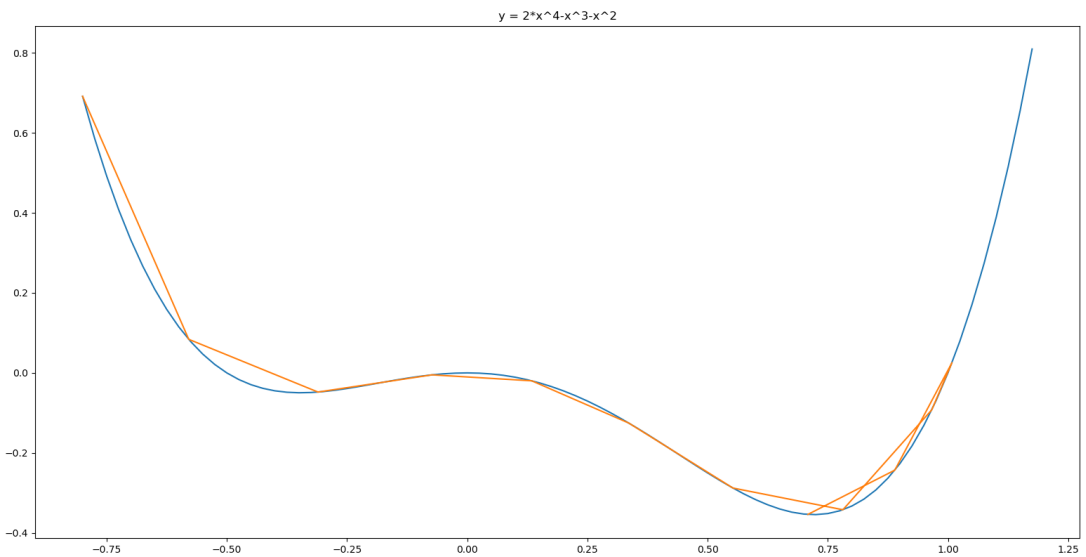
可以看出从-0.8开始迭代，依靠动量成功越过第一个次优解，发现无法越过最优解，折叠回来，最终收敛到最优解。对应代码如下

返回目录

Adam法

Adam实际上是把momentum和RMSprop结合起来的一种算法

假设N元函数f(x)，针对一个自变量研究Adam梯度下降的迭代过程，

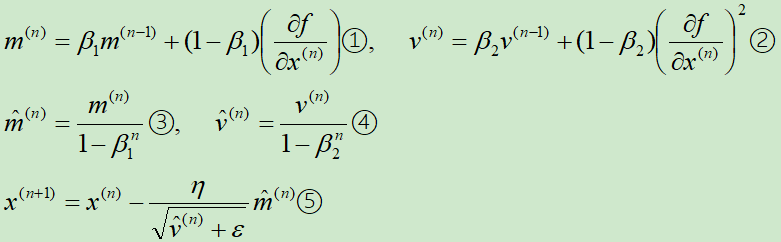
下面依次解释这五个式子：

在①式中，注意m(n)是反向的动量与梯度的和（而在Momentum中是正向动量与负梯度的和，因此⑤式对应的是减号）

在②式中，借鉴的是RMSprop的指数衰减

③和④式目的是纠正偏差

⑤式进行梯度更新

举例：使用Adagrad算法求y = x²的最小值点

导函数为h(x) = 2x

初始化x⁽⁰⁾ = 4，m⁽⁰⁾ = 0，v⁽⁰⁾ = 0，β₁=0.9，β₂=0.999，ε=10^-8，η = 0.001

第①次迭代：

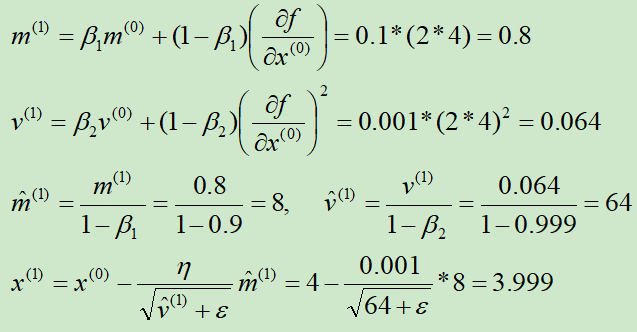
第②次迭代：

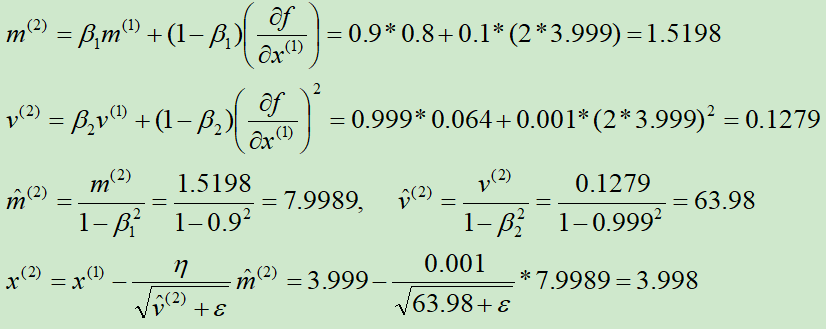
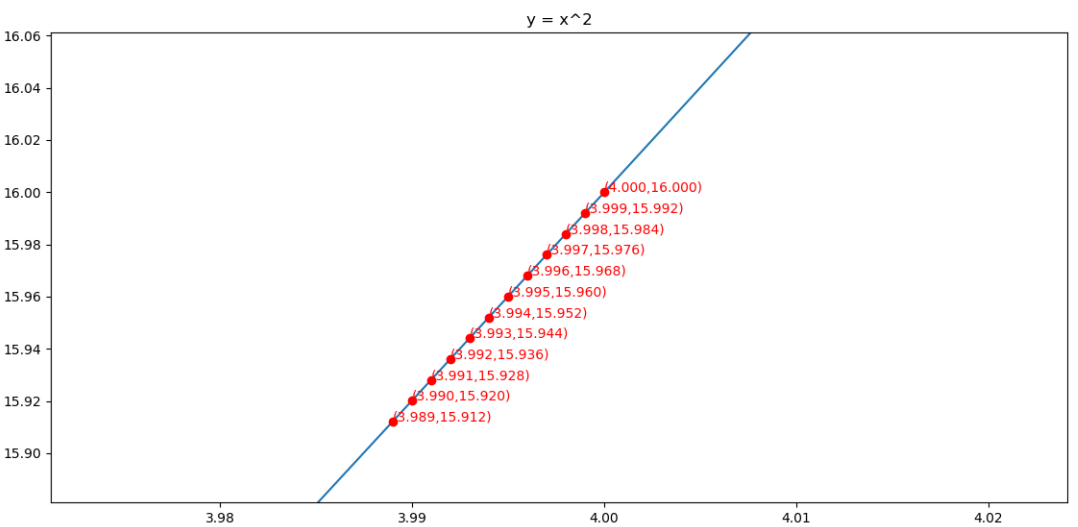
求解的过程如下图所示

对应代码为：

返回目录

参考资料

李宏毅——一天搞懂深度学习

深度学习中优化方法——momentum、Nesterov Momentum、AdaGrad、Adadelta、RMSprop、Adam

https://blog.csdn.net/u012328159/article/details/80311892

《图解深度学习与神经网络：从张量到TensorFlow实现》_张平