DBSCAN聚类

一、概述

  DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的聚类算法，簇集的划定完全由样本的聚集程度决定。聚集程度不足以构成簇落的那些样本视为噪声点，因此DBSCAN聚类的方式也可以用于异常点的检测。

二、算法原理

1.基本原理

  算法的关键在于样本的‘聚集程度’，这个程度的刻画可以由聚集半径和最小聚集数两个参数来描述。如果一个样本聚集半径领域内的样本数达到了最小聚集数，那么它所在区域就是密集的，就可以围绕该样本生成簇落，这样的样本被称为核心点。如果一个样本在某个核心点的聚集半径领域内，但其本身又不是核心点，则被称为边界点；既不是核心点也不是边界点的样本即为噪声点。其中，最小聚集数通常由经验指定，一般是数据维数+1或者数据维数的2倍。

  通俗地讲，核心点就是构成一个簇落的核心成员；边界点就是构成一个簇落的非核心成员，它们分布于簇落的边界区域；噪声点是无法归属在任何一个簇集的游离的异常样本。如图所示。

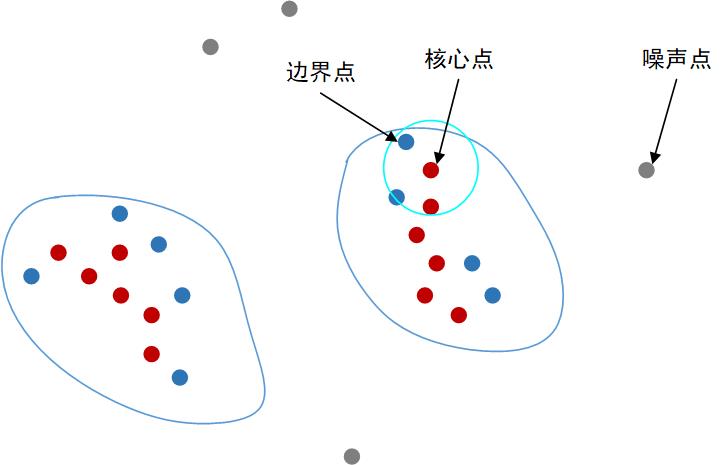
  对于聚成的簇集，这里有三个相关的概念：密度直达，密度可达，密度相连。

密度直达： 对一个核心点p，它的聚集半径领域内的有点q，那么称p到q密度直达。密度直达不具有对称性。

密度可达： 有核心点p1,p2,…,pn，非核心点q，如果pi到pi+1（i=1,2,…,n-1）是密度直达的，pn到q是密度直达的，那么称核心点pi(i=1,2,…,n)到其他的点是密度可达的。密度可达不具有对称性。

密度相连： 如果有核心点P，到两个点A和B都密度可达，那么称A和B密度相连。密度相连具有对称性。

  简单地讲，核心点到其半径邻域内的点是密度直达的；核心点到其同簇集内的点是密度可达的；同一个簇集里的成员间是密度相连的。

  由定义易知，密度直达一定密度可达，密度可达一定密度相连。密度相连就是对聚成的一个簇集最直接的描述。

2.算法描述

输入： 样本集D，聚集半径r，最小聚集数MinPts；

输出： 簇集C1，C2，…,Cn，噪声集O.

根据样本聚集程度，传播式地划定聚类簇，并将不属于任何一个簇的样本划入噪声集合。

（1）随机搜寻一个核心点p，

S1.从样本集D中随机选择一个未归入任何集合的且未被标记的样本对象p

S2.计算p的r邻域大小\(\left| N_r(p) \right|\)

若\(\left| N_r(p) \right|\geq MinPts\) ，则标记为核心点；否则，标记为非核心点，并选择其他的点进行判别.

S3.重复上面的步骤，直至找到一个核心点；若未找到，将未归集的样本划入噪声集O.

（2）在核心点p处建立簇C，将r邻域内所有的点加入簇C.

（3）对邻域内所有未被标记的点迭代式进行考察，扩展簇集.

若一个邻域点q为核心点，则将它领域内未归入集合的点加入簇C中.

（4）重复以上步骤，直至所有样本划入了指定集合；

（5）输出簇集C1，C2，…，Cn和噪声集合O。

3.优缺点

优势：

  1.可以发现任意形状的簇，适用于非凸数据集；

  2.可以进行异常检测；

  3.不需要指定簇数，根据样本的密集程度适应性地聚集。

不足：

  1.当样本集密度不均匀，不同簇中的平均密度相差较大时，效果较差；

  2.聚集半径和最小聚集数两个参数需人工指定。

三、示例

  假设二维空间中有下列样本，坐标为

(1,2),(1,3),(3,1),(2,2),(9,8),(8,9),(9,9),(18,18)

  由DBSCAN算法完成聚类操作。

过程演算：

  由经验指定参数聚集半径r=2，最小聚集数MinPts=3。

（1）随机搜寻一个核心点，若不存在，返回噪声集合。

  考察点(1,2)，它到各点的距离分别为

  在它的r邻域内，包括了自身在内的共三个样本点，达到了MinPts数，因此(1,2)为核心点。

（2）在核心点(1,2)处建立簇C1，原始簇成员为r邻域内样本：(1,2)、(1,3)、(2,2)。

（3）对簇落C1成员迭代式进行考察，扩展簇集。

  先考察(1,3)，它到各点的距离分别为

  在它的r邻域内，包括了自身在内的共三个样本点，达到了MinPts数，因此(1,3)为核心点，它邻域内的样本均已在簇C1中，无需进行操作。

  再考察(2,2)，它到各点的距离分别为

  在它的r邻域内，包括了自身在内的共四个样本点，达到了MinPts数，因此(2,2)为核心点，将它领域内尚未归入任何一个簇落的点(3,1)加入簇C1。

  再考察(3,1)，它到各点的距离分别为



  在它的r邻域内，包括了自身在内的共两个样本点，因此(3,1)是非核心点。

  考察结束，簇集C1扩展完毕。

（4）在其余未归簇的样本点中搜寻一个核心点，若不存在，返回噪声集合。

  考察点(9,8)，它到各点的距离分别为



  在它的r邻域内，包括了自身在内的共三个样本点，达到了MinPts数，因此(9,8)为核心点。

（5）在核心点(9,8)处建立簇C2，原始簇成员为r邻域内样本：(9,8)、(8,9)、(9,9)。

（6）对簇落C2成员迭代式进行考察，扩展簇集。

  先考察(8,9)，它到各点的距离分别为

  在它的r邻域内，包括了自身在内的共三个样本点，达到了MinPts数，因此(8,9)为核心点，它邻域内的样本均已在簇C2中，无需进行操作。

再考察(9,9)，它到各点的距离分别为

  在它的r邻域内，包括了自身在内的共三个样本点，达到了MinPts数，因此(9,9)为核心点。它邻域内的样本均已在簇C2中，无需进行操作。

考察结束，簇集C2扩展完毕。

（7）在其余未归簇的样本点中搜寻一个核心点，若不存在，返回噪声集合。

  其余未归簇的样本点集合为{(18,18)}，考察(18,18)，它到各点的距离分别为



  在它的r邻域内，包括了自身在内的共一个样本点，未达到MinPts数，因此(18,18)为非核心点。其余未归簇的样本中不存在核心点，因此归入噪声集O={(18,18)}。

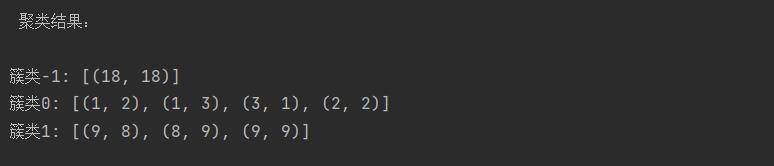
（8）输出聚类结果

  簇类C1：{(1,2),(1,3),(3,1),(2,2)}

  簇类C2：{(9,8),(8,9),(9,9)}

  噪声集O：{(18,18)}

四、Python实现

示例的Python实现。

'''
功能：用python实现DBSCAN聚类算法。
'''
from sklearn.cluster import DBSCAN
import numpy as np
import matplotlib.pyplot as plt

# 初始化数据
data = np.array([(1,2),(1,3),(3,1),(2,2),
              (9,8),(8,9),(9,9),
              (18,18)])

# 定义DBSCAN模型
dbscan = DBSCAN(eps=2,min_samples=3)

# 计算数据，获取标签
labels = dbscan.fit_predict(data)

# 定义颜色列表
colors = ['b','r','c']
T = [colors[i] for i in labels]

# 输出簇类
print('\n 聚类结果： \n')
ue = np.unique(labels)
for i in range(ue.size):
    CLS = []
    for k in range(labels.size):
        if labels[k] == ue[i]:
            CLS.append(tuple(data[k]))
    print('簇类{}:'.format(ue[i]),CLS)

# 结果可视化
plt.figure()
plt.scatter(data[:,0],data[:,1],c=T,alpha=0.5)  # 绘制数据点
plt.show()

运行结果：

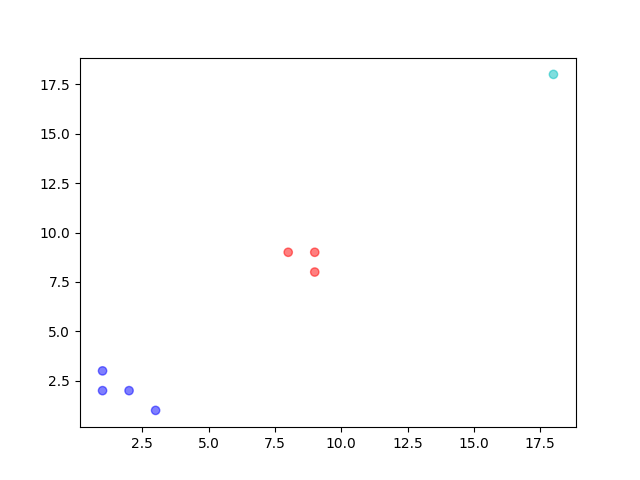
End.