遗传算法解决航路规划问题（MATLAB）

遗传算法

文章部分图片和思路来自司守奎，孙兆亮《数学建模算法与应用》第二版

定义：遗传算法是一种基于自然选择原理和自然遗传机制的搜索（寻优）算法，模拟自然界中的声明进化机制，在人工系统中实现特定目标的优化。

本质其实就是群体搜索技术，根据适者生存的原则逐代进化，最终得到最优解或近似最优解。

操作步骤

1. 产生初始群体（一般就是随机产生，但是也可以做一些操作，使得初始群体稍微优质一些，比如改良圈算法）
2. 求个体的适应度，即和最优解的距离
3. 根据适者生存的原则选择优良个体并两两配对
4. 通过随机交叉或随机变异得到下一代群体
5. 按照第四步的方法逐代进化
6. 满足进化终止条件

实现中需要注意

根据具体问题确定一种编码方式，能用数值或字符串表示可行解域的每一个解

需要确定适应度函数，即所需求解的目标函数

各种参数需要定义，如群体规模，交叉概率，变异概率，终止条件

模型操作方法

编码

采用十进制编码，用随机数列作为染色体

初始种群（改良圈）

对于随机产生的编码序列，交换u和v之间的顺序，得到的新路径和原路径代入目标函数计算，如果新路径得到的值更小则用新的路径替换，直到不能修改为止。

更小是因为本题求解的是最短路径越短越好

交叉

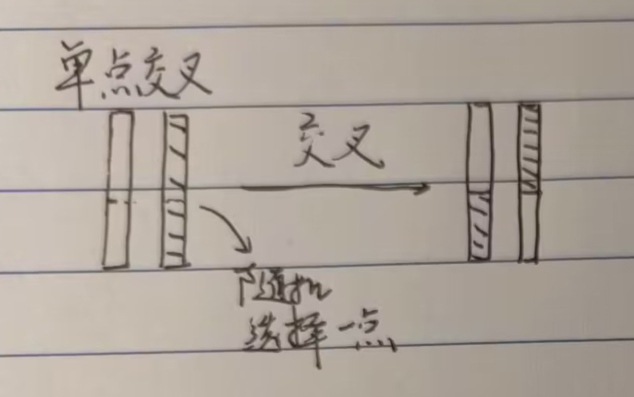
变异

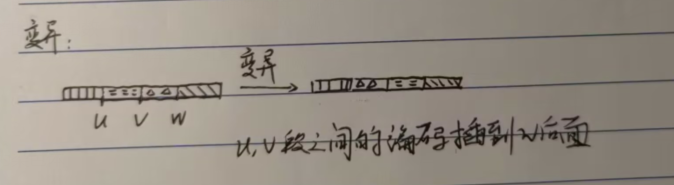
选择

选择与目标函数最接近的个体进化到下一代

代码

这里解决的问题是从经纬度[70,40]出发，走完100个地址的最短路径

这里的100个地址的经纬度直接随机生成了

random_matrix = rand(25, 8);

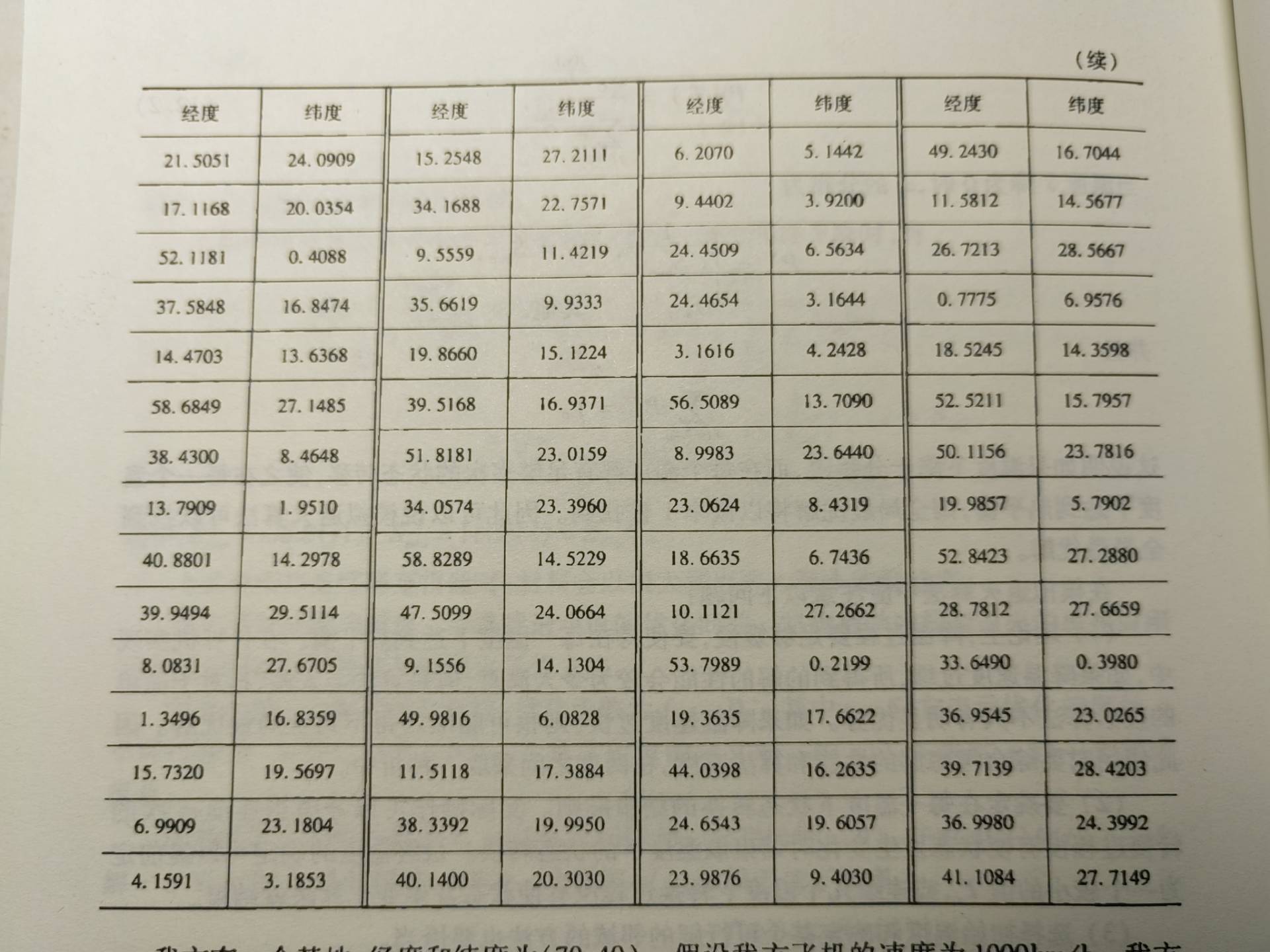
是以这样的方式储存在txt里

clc,clear
sj0=load('the2023_7_9\sj.txt'); % 加载一百个目标的数据
x=sj0(:,1:2:8); x=x(:);
y=sj0(:,2:2:8); y=y(:);
sj=[x,y];
d1=[0,0]; % 初始位置
sj=[d1;sj;d1];
sj=sj*pi/180; % 转化为弧度制

d=zeros(102); % 距离矩阵d初始化 102*102
 for i=1:101
     for j=(i+1):102
         d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
     end
 end
 d=d+d'; % 上三角的d和它的转置相加就得到了对称阵
 w=50;g=100; % 种群数50，进化代数100
 rand('state',sum(clock)); % 初始化随机数发生器
 %% 改良圈优化
 for k=1:w
     c=randperm(100); % 产生1-100的随机排列
     c1=[1,c+1,102]; % 初始解
     for t=1:102 % 此循环是修改圈
         flag=0; % 退出修改圈的标志
         for m=1:100
             for n=(m+2):101
                 if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
                     % 修改圈
                     c1(m+1:n)=c1(n:-1:m+1);
                     flag=1;
                 end
             end
         end
         if flag==0
             J(k,c1)=1:102; break; % 记录下当前较好的解并退出当前层循环
         end
     end
 end
J(:,1)=0;J=J/102; % 转换成[0,1]区间
 %% 进行遗传算法操作
 for k=1:g
     A=J; % 子代A的初始染色体
     c=randperm(w);
     % 产生交叉操作的染色体对
     for i=1:2:w
         F=2+floor(100*rand(1)); % 产生交叉操作的开始地址
         temp=A(c(i),F:102);
         A(c(i),F:102)=A(c(i+1),F:102); % 交叉操作
         A(c(i+1),F:102)=temp;
     end
     by=[]; % ?先初始化以防止出现空地址
     while isempty(by)
         by=find(rand(1,w)<0.1); % 产生变异操作的地址 ？
     end
     B=A(by,:); % 产生变异操作的初始染色体
     for j=1:length(by)
         bw=sort(2+floor(100*rand(1,3))); % 产生变异操作的三个地址
         B(j,:)=B(j,[1:bw(1)-1, bw(2)+1:bw(3), bw(1):bw(2), bw(3)+1:102]); % 交换位置
     end
     G=[J;A;B]; % 父代和子代种群结合在一起
     [SG,ind1]=sort(G,2); % 把染色体翻译成1，...102的序列indl
     num=size(G,1);long=zeros(1,num); % 路径的初始长度
     for j=1:num
         for i=1:101
            long(j)=long(j)+d(ind1(j,i),ind1(j,i+1)); % 计算每条路径长度
         end
     end
     [slong,ind2]=sort(long); % 对路径长度从小到大排序
     J=G(ind2(1:w),:); % 精选前w个较短路径对应的染色体
 end

path=ind1(ind2(1),:);flong=slong(1); % 解的路径和长度
xx=sj(path,1);yy=sj(path,2);
plot(xx,yy,'-o');

遗传算法的改进

遗传算法作为现代优化算法之一主要特点是对于非线性极值问题能以概率1跳出局部最优解找到全局最优解。这样的特性全都基于算法中的交叉和变异。

在传统的算法结构中，变异是在交叉的基础上进行，认为变异只是一个生物学背景机制。

交叉方法方面，上述算法使用的是单点交叉（随机选取某一点，该点右端的遗传信息全都交换）。

具体改进思路

1. 将变异操作从交叉操作中独立出来，作为一个单独的，并列与交叉操作的寻优操作
2. 混沌与遗传操作联系在一起
3. 以“门当户对”的原则进行个体间的交配，并采用单点交叉，确保算法收敛速度
4. 利用混沌序列对染色体中多个基因进行变异，防止算法早熟

模型及算法

交叉操作

对父代以适应度函数值进行排序，目标函数值小的之间相互配对，目标函数值大的之间配对，然后利用混沌序列确定交叉点的位置。

比如：

O1=a1-a2-a3-a4-a5---a102

O2=b1-b2-b3-b4-b5---b102

进行交叉操作

采用logistic混沌序列

x(n+1)=4x(n)[1-x(n)]产生一个2-101之间的正整数

这里是怎么产生的呢：

1. 取一个(0,1)区间上的随机数作为初始值【比如0.6】
2. 利用x(n+1)=4x(n)[1-x(n)]运算一次产生一个(0,1]区间上的值，称为混沌值（简单的求导运算就可以证明一定是在这个区间内）【计算得0.96】
3. 将0.96保存一下，下一次迭代的初值就不是随机取值了，而是0.96了，【第三代根据0.96来计算混沌值，即0.1536】
4. 这些(0.1)区间的值乘以100+2，最后取整，得到的数字就从那个位置开始进行单点交叉【比如0.6*100+2=62，那就从62开始交叉】
5. 最后得到O1=a1-a2-a3---b62---b102, O2=b1-b2-b3---a62---a102

变异操作

变异算子的设置：

给定一个变异率比如0.02之类，随机地选取两个2-101之间的整数，这两个位置进行变异，同样是使用混沌序列。

改进的遗传代码

tic % 计时开始
clc,clear
sj0=load('the2023_7_9\sj.txt'); % 加载一百个目标的数据
x=sj0(:,1:2:8); x=x(:);
y=sj0(:,2:2:8); y=y(:);
sj=[x,y];
d1=[40,70]; % 初始位置
sj=[d1;sj;d1];
sj=sj*pi/180; % 转化为弧度制

d=zeros(102); % 距离矩阵d初始化 102*102
 for i=1:101
     for j=(i+1):102
         d(i,j)=6370*acos(cos(sj(i,1)-sj(j,1))*cos(sj(i,2))*cos(sj(j,2))+sin(sj(i,2))*sin(sj(j,2)));
     end
 end
 d=d+d'; % 上三角的d和它的转置相加就得到了对称阵
 w=50;g=100; % 种群数50，进化代数100
 rand('state',sum(clock)); % 初始化随机数发生器
 %% 改良圈优化
 for k=1:w
     c=randperm(100); % 产生1-100的随机排列
     c1=[1,c+1,102]; % 初始解
     for t=1:102 % 此循环是修改圈
         flag=0; % 退出修改圈的标志
         for m=1:100
             for n=(m+2):101
                 if d(c1(m),c1(n))+d(c1(m+1),c1(n+1))<d(c1(m),c1(m+1))+d(c1(n),c1(n+1))
                     % 修改圈
                     c1(m+1:n)=c1(n:-1:m+1);
                     flag=1;
                 end
             end
         end
         if flag==0
             J(k,c1)=1:102; break; % 记录下当前较好的解并退出当前层循环
         end
     end
 end
J(:,1)=0;J=J/102; % 转换成[0,1]区间
 %% 进行遗传算法操作
 for k=1:g
     A=J; % 子代A的初始染色体
     c=randperm(w);
     % 产生交叉操作的染色体对
     for i=1:2:w

        ch1(1)=rand; % 混沌序列的初始值
        for j=2:50
            ch1(j)=4*ch1(j-1)*(1-ch1(j-1)); % 迭代产生混沌序列
        end
        ch1=2+floor(100*ch1) %交叉地址
        temp=A(i,ch1);
        A(i,ch1)=A(i+1,ch1);
        A(i+1,ch1)=temp;
     end
     by=[]; % ?先初始化以防止出现空地址
     while isempty(by)
         by=find(rand(1,w)<0.1); % 产生变异操作的地址 ？
     end
     num1=length(by);B=J(by,:); % 产生变异操作的初始染色体
     ch2=rand; % 另一个混沌序列
     for t=2:2*num1
         ch2(t)=4*ch2(t-1)*(1-ch2(t-1));
     end
     for j=1:num1
         bw=sort(2+floor(100*rand(1,2))); % 产生变异操作的两个地址
         B(j,bw)=ch2([j,j+1]);
     end

     G=[J;A;B]; % 父代和子代种群结合在一起
     [SG,ind1]=sort(G,2); % 把染色体翻译成1，...102的序列indl
     num2=size(G,1);long=zeros(1,num2); % 路径的初始长度
     for j=1:num2
         for i=1:101
            long(j)=long(j)+d(ind1(j,i),ind1(j,i+1)); % 计算每条路径长度
         end
     end
     [slong,ind2]=sort(long); % 对路径长度从小到大排序
     J=G(ind2(1:w),:); % 精选前w个较短路径对应的染色体
 end

path=ind1(ind2(1),:);flong=slong(1) % 解的路径和长度
toc % 计时结束
xx=sj(path,1);yy=sj(path,2);
plot(xx,yy,'-o');