Self-Attention 和 Transformer

1.Self-Attention

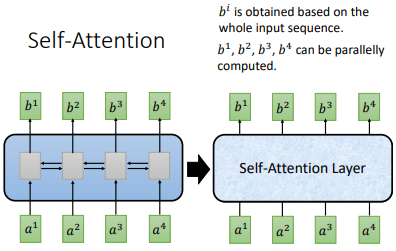
之前的RNN输入是难以并行化的，我们下一个输入可能依赖前一个输出，只有知道了前面的输出才能计算后面的输出。

于是提出了 self-attention ，但是这时候 $b^{i}$ 能够并行化计算

论文地址：https://arxiv.org/pdf/1706.03762.pdf

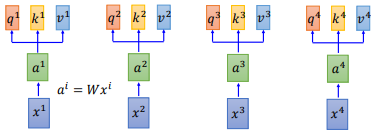
我们的输入 $x^{i}$，先经过一个Embedding，变成 $a^{i}$ ，然后丢进 self-attention 层中。如上图所示。

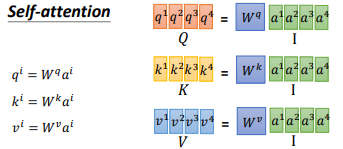
在self-attention中，我们的 $a^{i}$ 都乘上3个不同的矩阵，进行 transformation，得到3个不同的向量，分别是 $q$、$k$ 和 $v$。

$q$ 是query，它要去match的。$k$ 是key，用来被 $q$ match的；$v$ 是value，它是要被抽取出来的information。现在我们的每一个timestamp都有一个 $q$、$k$ 和 $v$ 这3个不同的向量。

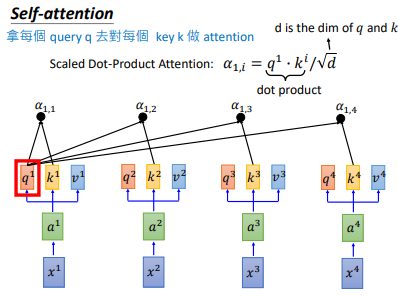
接下来我们对拿每一个 $q$ 对每一个 $k$ 做attention。如上图所示，$q^{1}$ 和 $k^{1}$ 做attention，得到 $\alpha _{1,1}$，下标（1,1）表示 $q^{1}$ 和 $k^{1}$ 的attention

attention有许多算法，它做的本质事情就是 吃 两个向量，输出一个分数，这个分数表明两个向量有多匹配

然后 $q^{1}$ 和 $k^{i}$ 计算得到 $\alpha _{1,i}$ ，计算公式和计算示意图如上图所示。然后我们会把得到的 $\alpha _{1,i}$ 经过一个softmax，得到 $\hat{\alpha }_{1,i}$，如下图所示

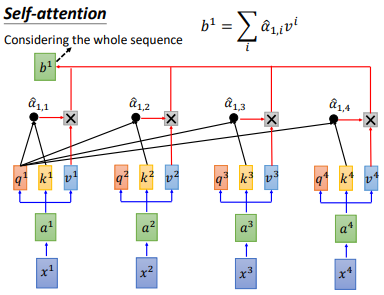
得到 $\hat{\alpha }_{1,i}$ 后，让 $\hat{\alpha }_{1,i}$ 分别乘以 $v^{i}$后累加，得到 $b^{1}$，我们输出 sequence 的第一个向量就是 $b^{1}$。但可以发现我们产生 $b^{1}$ 就已经使用了整个 sequence 的信息。

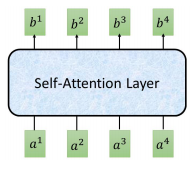
self-attention 输入是一个 sequence，输出也是sequence

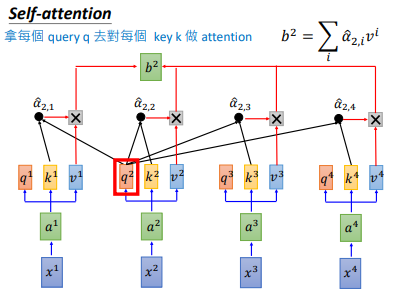
其他 $b^{i}$ 也是同样的计算流程，可以并行计算，比如 $b^{2}$，这样就得到了输出sequence的第二个向量

论文中的公式：$Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V$

Q、K、V是矩阵各个向量拼接而成的矩阵，整个矩阵计算的示意图如下图所示

从上面可以看到，self-attention 就是一连串矩阵运算。

2.Multi-Head Attention

我们用 2 heads 的情况举例，这种情况下，我们的 $q^{i}$ 会分裂成两个—— $q^{i,1}$ 和 $q^{i,2}$。

实际中 head 的数目也是参数，可以调

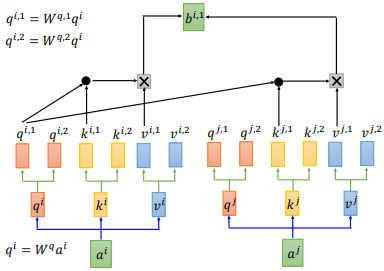
然后 $q^{i,1}$ 和 $k^{i,1}$ 、$k^{j,1}$ 分别计算 attention，最后计算出 $b^{i,1}$，如上图所示。用同样的步骤计算出 $b^{i,1}$ 和 $b^{i,2}$，把它们两个 concat 后乘以一个矩阵 $W^{o}$ ，得到 $b^{i}$。

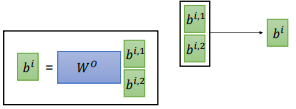
论文中的公式：$Multi-Head(Q,K,V)=Concat(head_{1},...,head_{h})W^{o}$

其中$head_{i}=Attention(QW^{Q}_{i},KW^{K}_{i},VW^{V}_{i})$

但是 self-attention 没有用到  sequence 的位置信息

所以在输入 $x^{i}$ 经过 transformation 得到 $a^{i}$ 后，还要加上一个 $e^{i}$， $e^{i}$ 是人工设置的，这个 $e^{i}$ 代表了位置信息。

论文3.5节Positional Encoding

定义这个向量的方式有多种多样。 比如，用 $p^{i}$ 表示位置信息，让 $p^{i}$ 和一个矩阵 $W^{p}$ 相乘得到的就是我们的 $e^{i}$

下面是做 self-attention 的一个动态示意图。可以看到 encoder 阶段 self-attention 是并行的且用到了所有单词的信息。

3.transformer

transformer 模型架构图如下图所示，对 encoder 和 decoder 使用了 self-attention 机制

左边是 encoder ，右边是 decoder

encoder 是左边灰色的图块，它可以重复 N 次，在 encoder 中，有一个 Multi-Head Attention 层，根据前面了解到的信息。这层的输入是一个 sequence，输出也是一个 sequence。如下图所示。

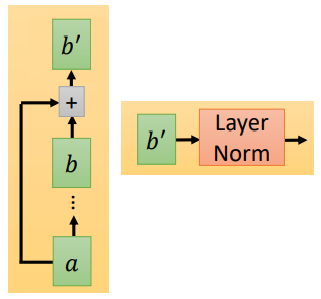
然后再经过 Add & Norm。Add 指我们会把 Multi-Head Attention 的输入和输出加起来得到 $b'$，Norm指我们会把得到的 $b'$ 做 Layer Norm。

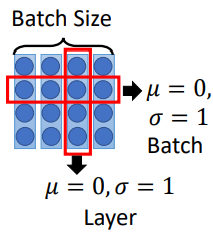
Layer Norm 和 Batch Norm 的不同：

在做 Batch Norm 的时候，在同一个 batch 里面，对不同 data 同样的 dimension 做 normalization，希望整个 batch 里面同一个 dimension 的均值为0，方差为1。

Layer Norm 是给一组 data，我们希望不同 dimension 的均值为0，方差为1。如下图所示

之后再经过 Feed Forward ，它对刚刚的输出进行处理，然后再经过一个 Add & Norm。

下面看看右边的 decoder ，它也可以重复 N 次。

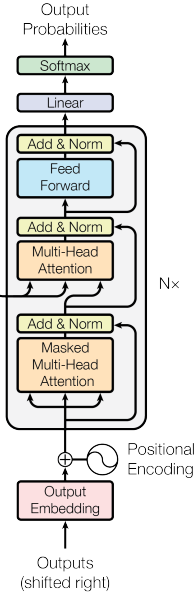
它的输入是上一个 tiemstamp 的输出，同样经过 embedding 和 positional encoding 后进入 decoder 中。decoder 的第一层是 Masked Multi-Head Attention，Masked 是说我们在做 self-attention 的时候这个 decoder 只会 attend 到它已经产生出来的 sequence。然后经过 Add & Norm ，再经过 Multi-Head，这个 Multi-Head Attention 会 attend 到之前 encoder 的输出，……，然后输出。

上面这张图显示了英语到法语翻译（eight attention heads之一）训练的 transformer 第5层到第6层中encoder 的 “it” 一词的 self-attention 分布。

可以看到 “it” attend 到了 animal，可以看到我们的模型自动学到了在做 attention 时，“it” 要 attend 到 “animal”。

当我们只改动左边的一个单词，把 tired 改为 wide。这句子里 “it” 再指动物，而是指 street，说它太宽了，我们的模型也能 attend 到 street。

详细文章：https://ai.googleblog.com/2017/08/transformer-novel-neural-network.html