P1140 相似基因

题目背景

大家都知道，基因可以看作一个碱基对序列。它包含了4种核苷酸，简记作A,C,G,T。生物学家正致力于寻找人类基因的功能，以利用于诊断疾病和发明药物。

在一个人类基因工作组的任务中，生物学家研究的是：两个基因的相似程度。因为这个研究对疾病的治疗有着非同寻常的作用。

题目描述

两个基因的相似度的计算方法如下：

对于两个已知基因，例如AGTGATG和GTTAG，将它们的碱基互相对应。当然，中间可以加入一些空碱基-，例如：

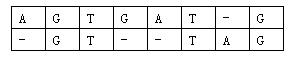
这样,两个基因之间的相似度就可以用碱基之间相似度的总和来描述，碱基之间的相似度如下表所示：

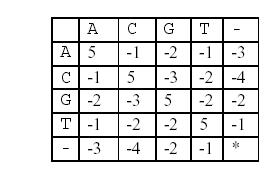
那么相似度就是：(-3)+5+5+(-2)+(-3)+5+(-3)+5=9。因为两个基因的对应方法不唯一，例如又有：

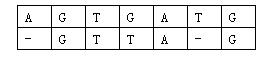
相似度为：(-3)+5+5+(-2)+5+(-1)+5=14。规定两个基因的相似度为所有对应方法中，相似度最大的那个。

输入输出格式

输入格式：

共两行。每行首先是一个整数，表示基因的长度；隔一个空格后是一个基因序列，序列中只含A,C,G,T四个字母。1<=序列的长度<=100。

输出格式：

仅一行，即输入基因的相似度。

输入输出样例

输入样例#1：

7 AGTGATG
5 GTTAG

输出样例#1：

14

Solution：

　　本题是一道比较典型的$DP$。

　　我们先考虑定义状态，$f[i][j]$表示匹配到了$s1$的$i$位置和$s2$的$j$位置时，能匹配到的最大基因相似度，那么目标状态即$f[n][m]$。

　　转换碱基，将$A\leftrightarrow 0,C\leftrightarrow 1,G\leftrightarrow 2,T\leftrightarrow 3,-\leftrightarrow 4$，然后把$s1,s2$按上述方法映射为$a,b$，同时建立$w[5][5]$数组，$w[i][j]$表示$i-j$配对的值。

　　先考虑初始状态，$f[i][j],i\in [1,n],\;j\in [1,m]$初始化为负无穷，因为可以与空碱基匹配，所以初始时$f[i][0]=f[i-1][0]+w[a[i]][4],i\in [1,n]$表示$s1$的每位与空碱基配对的值，$f[0][i]=f[0][i-1]+w[b[i]][4],i\in [1,m]$含义同上。

　　再考虑中间状态转移，可以发现上一个状态向下一个状态转移时，只有三种情况：

　　1、$f[i][j]=max(f[i][j],f[i][j-1]+w[b[j]][4])$表示$s1_i$在$s2_j$位置时与空碱基配对;　　

　　2、$f[i][j]=max(f[i][j],f[i-1][j]+w[a[i]][4])$表示$s2_j$在$s1_i$位置时与空碱基配对;　　

　　3、$f[i][j]=max(f[i][j],f[i-1][j-1]+w[a[i]][b[j]])$表示$s1_i$和$s2_j$配对。

　　容易想到对于$s1$的每个位置，都可以与$s2$的每个位置匹配一次，所以整体枚举复杂度为$O(nm)$（$n$为$s1$长度，$m$为$s2$长度）。

　　最后输出目标状态$f[n][m]$就$OK$了。

代码：

#include<bits/stdc++.h>
#define il inline
#define ll long long
using namespace std;
const int inf=;
int n,m,f[][],a[],b[];
int w[][]=
{
    {,-,-,-,-},
    {-,,-,-,-},
    {-,-,,-,-},
    {-,-,-,,-},
    {-,-,-,-,}
};
char s1[],s2[];
il void change(char *s,int *a,int l){
    for(int i=;i<=l;i++){
        if(s[i]=='A')a[i]=;
        if(s[i]=='C')a[i]=;
        if(s[i]=='G')a[i]=;
        if(s[i]=='T')a[i]=;
    }
}
int main()
{
    scanf("%d%s%d%s",&n,s1+,&m,s2+);
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++)f[i][j]=-inf;
    change(s1,a,n),change(s2,b,m);
    for(int i=;i<=n;i++)f[i][]=f[i-][]+w[a[i]][];
    for(int i=;i<=m;i++)f[][i]=f[][i-]+w[b[i]][];
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++){
            f[i][j]=max(f[i][j],f[i][j-]+w[b[j]][]);
            f[i][j]=max(f[i][j],f[i-][j]+w[a[i]][]);
            f[i][j]=max(f[i][j],f[i-][j-]+w[a[i]][b[j]]);
        }
    cout<<f[n][m];
    return ;
}