【图论搜索】bzoj1064: [Noi2008]假面舞会

做到最后发现还是读题比赛；不过还是很好的图论题的

Description

一年一度的假面舞会又开始了，栋栋也兴致勃勃的参加了今年的舞会。今年的面具都是主办方特别定制的。每个参加舞会的人都可以在入场时选择一个自己喜欢的面具。每个面具都有一个编号，主办方会把此编号告诉拿该面具的人。为了使舞会更有神秘感，主办方把面具分为k (k≥3)类，并使用特殊的技术将每个面具的编号标在了面具上，只有戴第i 类面具的人才能看到戴第i+1 类面具的人的编号，戴第k 类面具的人能看到戴第1 类面具的人的编号。参加舞会的人并不知道有多少类面具，但是栋栋对此却特别好奇，他想自己算出有多少类面具，于是他开始在人群中收集信息。栋栋收集的信息都是戴第几号面具的人看到了第几号面具的编号。如戴第2号面具的人看到了第5 号面具的编号。栋栋自己也会看到一些编号，他也会根据自己的面具编号把信息补充进去。由于并不是每个人都能记住自己所看到的全部编号，因此，栋栋收集的信息不能保证其完整性。现在请你计算，按照栋栋目前得到的信息，至多和至少有多少类面具。由于主办方已经声明了k≥3，所以你必须将这条信息也考虑进去。

Input

第一行包含两个整数n, m，用一个空格分隔，n 表示主办方总共准备了多少个面具，m 表示栋栋收集了多少条信息。接下来m 行，每行为两个用空格分开的整数a, b，表示戴第a 号面具的人看到了第b 号面具的编号。相同的数对a, b 在输入文件中可能出现多次。

Output

包含两个数，第一个数为最大可能的面具类数，第二个数为最小可能的面具类数。如果无法将所有的面具分为至少3 类，使得这些信息都满足，则认为栋栋收集的信息有错误，输出两个-1。

Sample Input

【输入样例一】
6 5
1 2
2 3
3 4
4 1
3 5
【输入样例二】
3 3
1 2
2 1
2 3

Sample Output

【输出样例一】
4 4

【输出样例二】
-1 -1

HINT

100%的数据，满足n ≤ 100000, m ≤ 1000000。

题目分析

naive

首先会有一个很naive的想法：

对于无环的图找最大值：拓扑地从1开始标号dfs做下去，中途检查边$(u,v)$，若$v$已经被标号且$col_v≠col_u+1$，就是不合法的，随即输出"-1 -1"。

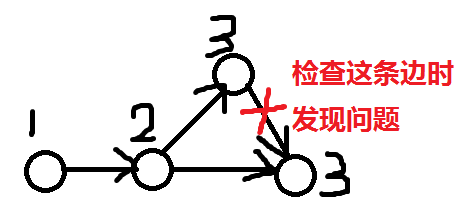
讲上去求的是最大值所以看上去很对劲是吧？

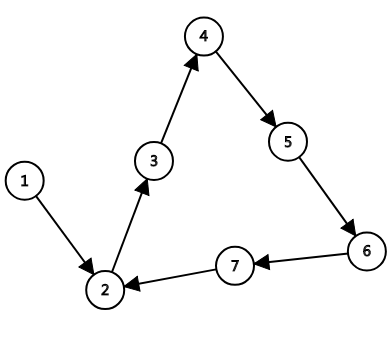
但是遇上这么一个环呢？7之后连的是2，所以判成无解。但是然而实际上$k=3$是成立的。

也就是说，简单地考虑“环缩点”或者“直接染色”是行不通的。

实际做法

学了tarjan之后不要在找环只想到tarjan！

这个问题其实建个反向边之后，可以分为两类：

有环的
没环的

没环的情况：树是很简单的，最大值就是所有树的最长链总和，最小值一定是3。

有环的情况：

DFS听上去很基础吧，但是切不要以为基础的东西就没什么用处。

这里依靠DFS找出每一个环的长度，并且注意到最大答案就是所有环长度的gcd。只要最终的$gcd≥3$，结合没环情况的下界可知环外其他树对答案不造成影响。

可能会想到环套环的情况。不过首先这个DFS要永久标记访问，复杂度是$O(n)$的，不会被卡；其次我们求的是环长度的gcd，并且如果答案合法，大环长度一定是小环的倍数，所以即便大环套在小环外，也不影响最终答案。

大致思路就是这样。

细节注意树的情况，最大值是所有树的最长链总和！

 #include<bits/stdc++.h>

 const int maxn = ;

 const int maxm = ;

 struct node

 {

     int id;

     std::vector<int> norEdge,difEdge;

 }a[maxn];

 int n,m,cnt,mn,mx,chain,ans;

 bool vis[maxn];

 std::pair<int, int> edges[maxm];

 int read()

 {

     char ch = getchar();

     int num = ;

     bool fl = ;

     for (; !isdigit(ch); ch = getchar())

         if (ch=='-') fl = ;

     for (; isdigit(ch); ch = getchar())

         num = (num<<)+(num<<)+ch-;

     if (fl) num = -num;

     return num;

 }

 int gcd(int x, int y){return !y?x:gcd(y, x%y);}

 void addedge(int x)

 {

     int u = edges[x].first, v = edges[x].second;

     a[u].norEdge.push_back(v), a[v].difEdge.push_back(u);

 }

 void dfs(int x, int lb)

 {

     if (vis[x]){

         ans = gcd(ans, abs(a[x].id-lb));　　　　//找到一个环了

         return;

     }

     a[x].id = lb, vis[x] = ;

     mn = std::min(mn, lb), mx = std::max(mx, lb);

     int sa = a[x].norEdge.size(), sb = a[x].difEdge.size();

     for (int i=; i<sa; i++)

         dfs(a[x].norEdge[i], lb+);　　　　　　//正向边

     for (int i=; i<sb; i++)

         dfs(a[x].difEdge[i], lb-);　　　　　　//反向边

     return;

 }

 int main()

 {

     // freopen("testdata.in","r",stdin);

     n = read(), m = read();

     for (int i=; i<=m; i++)

         edges[i].first = read(), edges[i].second = read();

     std::sort(edges+, edges+m+);　　　　　　//用pair存边方便去重

     addedge();

     for (int i=; i<=m; i++)

         if (edges[i]!=edges[i-])

             addedge(i);

     for (int i=; i<=n; i++)

         if (!vis[i]){　　　　//由于建了双向边，故不用考虑拓扑序

             dfs(i, );

             chain += mx-mn+;

             mn = mx = ;

         }

     if (ans >= ){　　　　//如果有环并且合法

         for (int i=; i<=ans/; i++)

             if (ans%i==){

                 printf("%d %d\n",ans,i);　　//找最小的答案——求最小约数

                 return ;

             }

         printf("%d %d\n",ans,ans);　　　　　 //最小答案还是ans

         return ;

     }

     if (!ans&&chain>=){

         printf("%d %d\n",chain,);

         return ;

     }　　　　　　　　　　//否则不合法，ans=1

     printf("-1 -1\n");

     return ;

 }

END