<题解>洛谷P3385 【模板】负环

题目链接

判断一张图中是否存在关于顶点1的负环:

可以用SPFA跑一遍，存在负环的情况就是点进队大于n次

因为在存在负环的情况下,SPFA会越跑越小，跑进死循环

在最差的情况下,存在的负环长度是“n+1个顶点”这么长

rt:

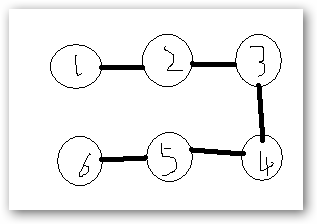
显然这是n个点长度,但不是环；

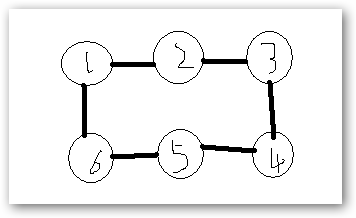
这就是一个环,n+1个点的长度;

所以代码很明了了,只需将一般SPFA改动一点饥渴
CODE:

#include<bits/stdc++.h>万能头，懒得打很多头文件
using namespace std;
//数据是骗人的，要开大..
const int maxn=;
//基本的变量或者数组都是：
queue<int > q;
bool visited[maxn];
int head[maxn],cnt,js[maxn],dis[maxn];
struct ppap {
    int next,to,dis;
} edge[maxn];
int t,n,m;
//快读部分
int read() {
    bool f=;
    char ch;
    int x=;
    ch=getchar();
    while(ch>''||ch<'') {
        if(ch=='-')
            f=!f;
        ch=getchar();
    }
    while(ch<=''&&ch>='') {
        x=x*+ch-'';
        ch=getchar();
    }
    return !f?x:-x;
}
//链式前向星添边
void add(int from,int to,int dis) {
    edge[++cnt].next=head[from];
    head[from]=cnt;
    edge[cnt].to=to;
    edge[cnt].dis=dis;
}
//和常见spfa一样，在其中判断条件即可
bool SPFA() {
    q.push();
    visited[]=;
    dis[]=;
    js[]=;
    while(!q.empty()) {
        int u=q.front();
        q.pop();
        visited[u]=;
        for(int i=head[u]; i; i=edge[i].next) {
            int v=edge[i].to;
            if(dis[v]>dis[u]+edge[i].dis) {
                dis[v]=dis[u]+edge[i].dis;
                if(visited[v]==) {
                    js[v]=js[u]+;
                    if(js[v]>n) return true;
                    visited[v]=;
                    q.push(v);
                }
            }
        }
    }
    return false;
}

int main() {
    t=read();
    while(t--) {
        n=read(),m=read();
        memset(head,,sizeof head);
        memset(js,,sizeof js);
        memset(edge,,sizeof edge);
        memset(dis,0x3f,sizeof dis);
        memset(visited,,sizeof visited);
        //初始化
        for(int i=,a,b,w; i<=m; i++) {
            a=read(),b=read(),w=read();
            add(a,b,w);
            if(w>=)
                add(b,a,w);
        }
        if(SPFA()) cout<<"YE5"<<"\n";
        else cout<<"N0"<<"\n";
    }
    return ;//平淡的结束
}

评测记录