[洛谷P3941]:入阵曲（前缀和+桶）

题目传送门

---

题目背景

丹青千秋酿，一醉解愁肠。
无悔少年枉，只愿壮志狂。

---

题目描述

小$F$很喜欢数学，但是到了高中以后数学总是考不好。
有一天，他在数学课上发起了呆；他想起了过去的一年。一年前，当他初识算法竞赛的时候，觉得整个世界都焕然一新。这世界上怎么会有这么多奇妙的东西？曾经自己觉得难以解决的问题，被一个又一个算法轻松解决。
小$F$当时暗自觉得，与自己的幼稚相比起来，还有好多要学习的呢。
一年过去了，想想都还有点恍惚。
他至今还能记得，某天晚上听着入阵曲，激动地睡不着觉，写题写到鸡鸣时分都兴奋不已。也许，这就是热血吧。

也就是在那个时候，小$F$学会了矩阵乘法。让两个矩阵乘几次就能算出斐波那契数列的第$10^{100}$项，真是奇妙无比呢。
不过，小$F$现在可不想手算矩阵乘法——他觉得好麻烦。取而代之的，是一个简单的小问题。他写写画画，画出了一个$n\times m$的矩阵，每个格子里都有一个不超过$k$的正整数。
小$F$想问问你，这个矩阵里有多少个不同的子矩形中的数字之和是$k$的倍数？如果把一个子矩形用它的左上角和右下角描述为$(x_1,y_1,x_2,y_2)$，其中$x_1\leqslant x_2,y_1\leqslant y_2$​；那么，我们认为两个子矩形是不同的，当且仅当他们以$(x_1,y_1,x_2,y_2)$表示时不同；也就是说，只要两个矩形以$(x_1,y_1,x_2,y_2)$表示时相同，就认为这两个矩形是同一个矩形，你应该在你的答案里只算一次。

---

输入格式

从标准输入中读入数据。
输入第一行，包含三个正整数$n,m,k$。
输入接下来$n$行，每行包含$m$个正整数，第$i$行第$j$列表示矩阵中第$i$行第$j$列中所填的正整数$a_{i,j}$​。

---

输出格式

输出到标准输出中。
输入一行一个非负整数，表示你的答案。

---

样例

样例输入1：

2 3 2
1 2 1
2 1 2

样例输出1：

6

样例输入2：

10 10 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1

样例输出2：

3025

---

数据范围与提示

样例$1$说明：

这些矩形是符合要求的：
$(1,1,1,3)$，$(1,1,2,2)$，$(1,2,1,2)$，$(1,2,2,3)$，$(2,1,2,1)$，$(2,3,2,3)$。

数据范围：

子任务会给出部分测试数据的特点。如果你在解决题目中遇到了困难，可以尝试只解决一部分测试数据。
每个测试点的数据规模及特点如下表：

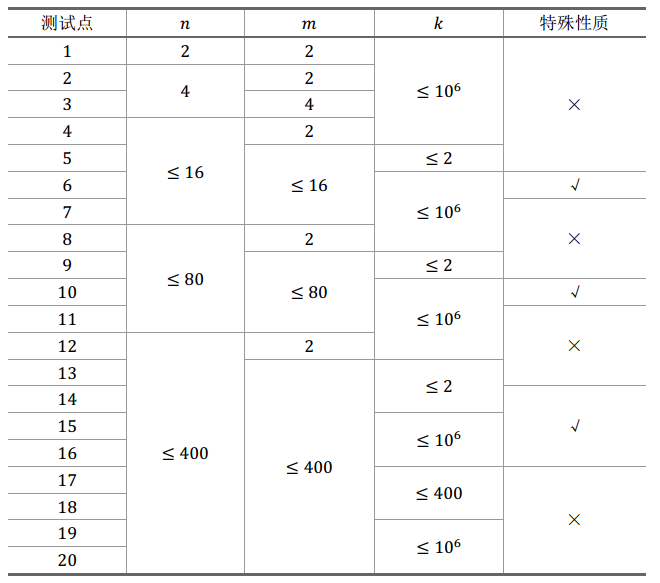
特殊性质：保证所有$a_{i,j}$均相同。

---

题解

$15\%$算法：

官方题解说是手动枚举，在此不做过多赘述。

时间复杂度：$\Theta(1)$。

期望得分：$15$分。

实际得分：$15$分。

$25\%$算法：

考虑特殊性质，可以枚举矩形的边长，然后看当前这个矩形的和是否是$k$的倍数，如果是的话$\Theta(1)$求出有多少个这样的矩形，统计答案即可。

时间复杂度：$\Theta(n\times m)$。

期望得分：$25$分。

时间得分：$30$分（撞对了一个点）。

$45\%$算法：

暴力枚举左下和右上端点，再暴力求和，比较。

时间复杂度：$\Theta(n^6)$。

期望得分：$45$分。

实际得分：$45$分。

$60\%$算法：

利用二位前缀和，让暴力球和的操作变为$\Theta(1)$。

时间复杂度：$\Theta(n^4)$。

期望得分：$60$分。

实际得分：$60$分。

$100\%$算法：

发现枚举再$ans++$肯定会超时，于是考虑不枚举。

观察到在$\mod k$意义下的前缀和，任取两个相减一定也是$k$的倍数。

于是问题转化为统计前缀和中$\equiv k$的数的对数。

直接对于每个余数统计个数即可，枚举所有连续的列压到一行处理。

时间复杂度：$\Theta(n^3)$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

$25\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m,mod;
int Map[500][500];
long long ans;
int main()
{
	scanf("%d%d%d",&n,&m,&mod);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&Map[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			if(!((1LL*i*j*Map[i][j])%mod))
				ans+=1LL*(n-i+1)*(m-j+1);
	cout<<ans;
	return 0;
}

$45\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m,mod;
int Map[500][500],wzc[500],cnt[1000001];
long long ans;
int main()
{
	scanf("%d%d%d",&n,&m,&mod);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			scanf("%d",&Map[i][j]);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=i;k<=n;k++)
				for(int l=j;l<=m;l++)
				{
					int sum=0;
					for(int x=i;x<=k;x++)
						for(int y=j;y<=l;y++)
							sum+=Map[x][y];
					if(!(sum%mod))ans++;
				}
	cout<<ans;
	return 0;
}

$60\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m,mod;
int Map[500][500];
int ans;
int main()
{
	scanf("%d%d%d",&n,&m,&mod);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&Map[i][j]);
			Map[i][j]=(Map[i][j]+Map[i-1][j]+Map[i][j-1]-Map[i-1][j-1]+mod)%mod;
		}
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=i;k<=n;k++)
				for(int l=j;l<=m;l++)
					if(!((Map[k][l]-Map[k][j-1]-Map[i-1][l]+Map[i-1][j-1]+mod)%mod))
						ans++;
	cout<<ans<<endl;
	return 0;
}

$100\%$算法：

#include<bits/stdc++.h>
using namespace std;
int n,m,mod;
int Map[500][500],wzc[500],cnt[1000001];
long long ans;
int main()
{
	scanf("%d%d%d",&n,&m,&mod);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%d",&Map[i][j]);
			Map[i][j]=(Map[i][j]+Map[i-1][j]+Map[i][j-1]-Map[i-1][j-1]+mod)%mod;
		}
	for(int i=1;i<=n;i++)
		for(int j=i;j<=n;j++)
		{
			cnt[0]=1;
			for(int k=1;k<=m;k++)ans+=cnt[(wzc[k]=Map[j][k]+mod-Map[i-1][k])%=mod]++;
			for(int k=1;k<=m;k++)cnt[wzc[k]]=0;
		}
	cout<<ans;
	return 0;
}

---

rp++