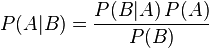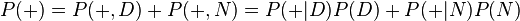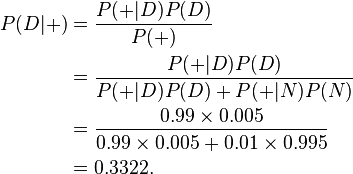Python 贝叶斯分类
很久的时间没有更新了,一是因为每天加班到比较晚的时间,另外,公司不能上网,回家后就又懒得整理,最近在看机器学习实战的书籍,因此才又决定重新拾起原先的博客!
今天讲的是第三章的贝叶斯分类方法,我们从一个简简单单的例子开始入手:首先看(1)图中的例子,假设有一个装了7块时候的罐子,其中3块时黑色的,4块时白色的,从中随机取出一个石头,那么这个石头是灰色的概率是多大?


(1) (2)
我们可以很轻易的计算出取出一个灰色球的概率是4/7,取出一个黑色球的概率是3/7,但是假如这些球被放在两个不同的罐子中,如图(2) :A中有3个黑球,2个灰球,B中有三个灰球,两个黑球。那我们从中取出一个灰球的概率是多大?我们很自然的联想到要首先知道是从A中去取还是从B中去取。
假设从A中取得概率为Pa,从B中取得概率为Pb,那么我们取出一个灰色球的概率为:
Pgray = ( 0.4 ) * Pa + ( 0.6 )* Pb
此时的0.4 和0.6 分别表示为从A和B桶中取出一个灰色球的概率,我们也称其为条件概率, 记为P(gray | A) = 0.4,P(gray|B) = 0.6
我们引出维基百科上关于贝叶斯公式的定义:
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。
其中P(A|B)是在B发生的情况下A发生的可能性。贝叶斯定理中,每个名词都有约定俗成的名称:
按这些术语,Bayes定理可表述为:
后验概率 = (相似度*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标准相似度(standardised likelihood),Bayes定理可表述为:
后验概率 = 标准相似度*先验概率
[例一(维基百科)]
贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(+)的概率为99%。而被检者不吸毒时,每次检测呈阴性(-)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。我们想知道,每位医学检测呈阳性的雇员吸毒的概率有多高?令“D”为雇员吸毒事件,“N”为雇员不吸毒事件,“+”为检测呈阳性事件。可得
- P(D)代表雇员吸毒的概率,不考虑其他情况,该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品,所以这个值就是D的先验概率。
- P(N)代表雇员不吸毒的概率,显然,该值为0.995,也就是1-P(D)。
- P(+|D)代表吸毒者阳性检出率,这是一个条件概率,由于阳性检测准确性是99%,因此该值为0.99。
- P(+|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为0.01,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1-99%。
- P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到:此概率 = 吸毒者阳性检出率(0.5% x 99% = 0.495%)+ 不吸毒者阳性检出率(99.5% x 1% = 0.995%)。P(+)=0.0149是检测呈阳性的先验概率。用数学公式描述为:
根据上述描述,我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+):
尽管我们的检测结果可靠性很高,但是只能得出如下结论:如果某人检测呈阳性,那么此人是吸毒的概率只有大约33%,也就是说此人不吸毒的可能性比较大。我们测试的条件(本例中指D,雇员吸毒)越难发生,发生误判的可能性越大。(这个相信能给曾经去体检结果非常不好的人一个乐观的消息)
[例二 (Machine Learn in Action)]
机器学习的一个非常重要的作用就是对文本进行分类,我们使用Python进行文本的分类
(未完待续)
参考:[1]刘未鹏 数学之美番外篇:平凡而又神奇的贝叶斯方法
[2] Machine Learn in Action, Peter Harrington
Python 贝叶斯分类的更多相关文章
- 朴素贝叶斯分类器及Python实现
贝叶斯定理 贝叶斯定理是通过对观测值概率分布的主观判断(即先验概率)进行修正的定理,在概率论中具有重要地位. 先验概率分布(边缘概率)是指基于主观判断而非样本分布的概率分布,后验概率(条件概率)是根据 ...
- 朴素贝叶斯分类算法介绍及python代码实现案例
朴素贝叶斯分类算法 1.朴素贝叶斯分类算法原理 1.1.概述 贝叶斯分类算法是一大类分类算法的总称 贝叶斯分类算法以样本可能属于某类的概率来作为分类依据 朴素贝叶斯分类算法是贝叶斯分类算法中最简单的一 ...
- (数据科学学习手札30)朴素贝叶斯分类器的原理详解&Python与R实现
一.简介 要介绍朴素贝叶斯(naive bayes)分类器,就不得不先介绍贝叶斯决策论的相关理论: 贝叶斯决策论(bayesian decision theory)是概率框架下实施决策的基本方法.对分 ...
- R&python机器学习之朴素贝叶斯分类
朴素贝叶斯算法描述应用贝叶斯定理进行分类的一个简单应用.这里之所以称之为“朴素”,是因为它假设各个特征属性是无关的,而现实情况往往不是如此. 贝叶斯定理也称贝叶斯推理,早在18世纪,英国学者贝叶斯(1 ...
- 《机器学习实战》基于朴素贝叶斯分类算法构建文本分类器的Python实现
============================================================================================ <机器学 ...
- 利用朴素贝叶斯分类算法对搜狐新闻进行分类(python)
数据来源 https://www.sogou.com/labs/resource/cs.php介绍:来自搜狐新闻2012年6月—7月期间国内,国际,体育,社会,娱乐等18个频道的新闻数据,提供URL ...
- 机器学习之路: python 朴素贝叶斯分类器 MultinomialNB 预测新闻类别
使用python3 学习朴素贝叶斯分类api 设计到字符串提取特征向量 欢迎来到我的git下载源代码: https://github.com/linyi0604/MachineLearning fro ...
- python实现一个朴素贝叶斯分类方法
1.公式 上式中左边D是需要预测的测试数据属性,h是需要预测的类:右边式子分子是属性的条件概率和类别的先验概率,可以从统计训练数据中得到,分母对于所有实例都一样,可以不考虑,所有只需 ,返回最大概率的 ...
- Python数据科学手册-机器学习:朴素贝叶斯分类
朴素贝叶斯模型 朴素贝叶斯模型是一组非常简单快速的分类方法,通常适用于维度非常高的数据集.因为运行速度快,可调参数少.是一个快速粗糙的分类基本方案. naive Bayes classifiers 贝 ...
随机推荐
- hdu 1257 一共要多少套拦截系统 (LIS)
给出导弹的高度 拦截的导弹会比上一次低 至少要几套拦截系统才能防御所有导弹 求一套系统能防御的最大导弹数: 反向LIS求一共要多少套:正向LIS Sample Input8 389 207 155 3 ...
- c++ primer 笔记 (二)
第二章笔记 (貌似记得有点多) 把负值赋给unsigned对象时完全合法的,其结果是该负数对该类型的取值个数求模后的值 -1 (对265求模) 255 float型只能保证6位 ...
- 【AtCoder】ARC082
C - Together 用一个数组记一下一个数给它本身,左右贡献都是1,看看哪个数的总贡献最大 #include <bits/stdc++.h> #define fi first #de ...
- Asp.Net Core 2.0 项目实战(2)NCMVC一个基于Net Core2.0搭建的角色权限管理开发框架
Asp.Net Core 2.0 项目实战(1) NCMVC开源下载了 Asp.Net Core 2.0 项目实战(2)NCMVC一个基于Net Core2.0搭建的角色权限管理开发框架 Asp.Ne ...
- KNN分类算法及python代码实现
KNN分类算法(先验数据中就有类别之分,未知的数据会被归类为之前类别中的某一类!) 1.KNN介绍 K最近邻(k-Nearest Neighbor,KNN)分类算法是最简单的机器学习算法. 机器学习, ...
- POJ 2752 (kmp求所有公共前后缀长度)
<题目链接> <转载于> 题目大意: 给出一个字符串str,求出str中存在多少子串,使得这些子串既是str的前缀,又是str的后缀.从小到大依次输出这些子串的长度.即输出该 ...
- win 7设置主机域名
1 Control Panel\Network and Internet\Network Connections right click Local Area Connection<proper ...
- Python中按值来获取指定的键
转自: https://blog.csdn.net/Jerry_1126/article/details/87907162 Python字典中的键是唯一的,但不同的键可以对应同样的值,比如说uid,可 ...
- 安卓 logcat设置 Android logcat Settings
安卓 logcat设置 Android logcat Settings 作者:韩梦飞沙 Author:han_meng_fei_sha 邮箱:313134555@qq.com E-mail: 3131 ...
- bzoj4503: 两个串 bitset
目录 题目链接 题解 代码 题目链接 bzoj4503: 两个串 题解 暴一发bitset f[i][j] 表示 S[1..i] 是否有个后缀能匹配 T[1..j] 那么假设 S[i+1] 能匹配 T ...