FP-growth算法思想和其python实现

第十二章 使用FP-growth算法高效的发现频繁项集

一．导语

FP-growth算法是用于发现频繁项集的算法，它不能够用于发现关联规则。FP-growth算法的特殊之处在于它是通过构建一棵Fp树，然后从FP树上发现频繁项集。

FP-growth算法它比Apriori算法的速度更快，一般能够提高两个数量级，因为它只需要遍历两遍数据库，它的过程分为两步：

1.构建FP树

2.利用FP树发现频繁项集

二．FP树

FP树它的形状与普通的树类似，树中的节点记录了一个项和在此路径上该项出现的频率。FP树允许项重复出现，但是它的频率可能是不同的。重复出现的项就是相似项，相似项之间的连接称之为节点连接，沿着节点连接我们可以快速的发现相似的项。

FP树中的项必须是频繁项，也就是它必须要满足Apriori算法。FP树的构建过程需要遍历两边数据库，第一遍的时候我们统计出所有项的频率，过滤掉不满足最小支持度的项；第二遍的时候我们统计出每个项集的频率。

三．构建FP树

1.要创建一棵树，首先我们需要定义树的数据结构。

这个数据结构有五个数据项，其中的parent表示父节点， children表示孩子节点， similar表示的相似项。

2.创建一棵Fp树

def createTree(dataSet, minSup=1):
    headerTable = {}
    # in order to catch the all the item and it's frequent
    for transaction in dataSet:
        for item in transaction:
            headerTable[item] = headerTable.get(item, 0) + dataSet[transaction]
    # delete the item which is not frequent item
    for key in headerTable.keys():
        if headerTable[key] < minSup:
            del(headerTable[key])
    frequentSet = headerTable.keys()
    # if the frequentSet is empty, then we can finish the program early
    if len(frequentSet) == 0:
        return None, None
    # initialize the begin link of headerTable is None
    for key in headerTable.keys():
        headerTable[key] = [headerTable[key], None]
    # initialize the fp-tree
    retTree = treeNode("RootNode", 1, None)
    # rearrange the transaction and add the transaction into the tree
    for transData, times in dataSet.items():
        arrangeTrans = {}
        for item in transData:
            if item in frequentSet:
                arrangeTrans[item] = headerTable[item][0]
        if len(arrangeTrans)>0:
            sortTrans = [v[0] for v in sorted(arrangeTrans.items(), key=lambda p:p[1], reverse=True)]
            updateTree(sortTrans, retTree, headerTable, times)
    return headerTable, retTree

def updateTree(sortTrans, retTree, headerTable, times):
    if sortTrans[0] in retTree.children:
        retTree.children[sortTrans[0]].inc(times)
    else:
        retTree.children[sortTrans[0]] = treeNode(sortTrans[0], times, retTree)
        if headerTable[sortTrans[0]][1] == None:
            headerTable[sortTrans[0]][1] = retTree.children[sortTrans[0]]
        else:
            updateHeader(headerTable[sortTrans[0]][1], retTree.children[sortTrans[0]])
    if len(sortTrans) > 1:
        updateTree(sortTrans[1::], retTree.children[sortTrans[0]], headerTable, times)

def updateHeader(nodeToTest, targetNode):
    while nodeToTest.similarNode != None:
        nodeToTest = nodeToTest.similarNode
    nodeToTest.similarNode = targetNode

四．从一棵FP树中挖掘频繁项集

从一棵FP树中挖掘频繁项集需要三个步骤，首先我们需要找到所有的条件模式基，其次是根据条件模式基创建一棵条件FP树，最后我们不断的重复前两个步骤直到树只包含一个元素项为止

首先我们要寻找条件模式基，那么什么是条件模式基呢？所谓的条件模式基就是以查找元素结尾的所有路径的集合。我们可以根据headertable中的nodelink来找到某一个元素在树中的所有位置，然后根据这些位置进行前缀路径的搜索。以下是它的python代码：

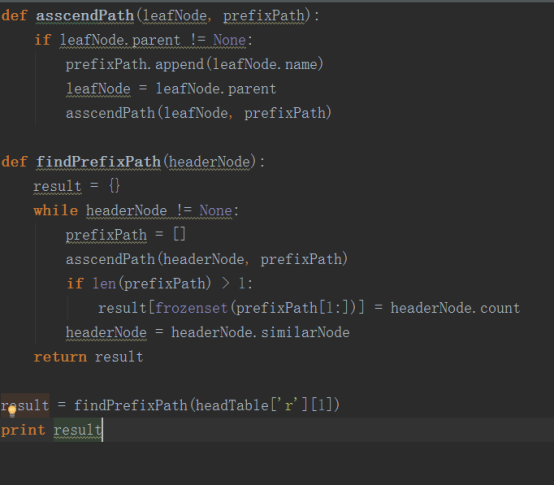
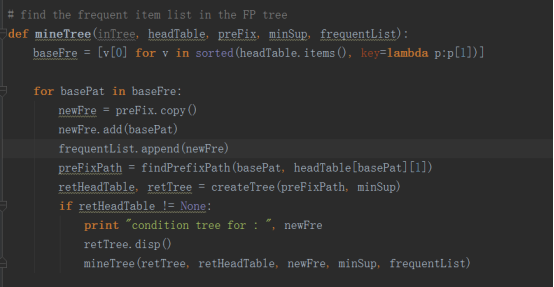
现在我们知道了如何找条件模式基，接下来就是创建一个FP条件树。在创建树之前我们首先要知道什么是FP条件树，所谓的FP条件树就是将针对某一个条件的条件模式基构建的一棵FP树。以下是python代码

五．一个浏览新闻共现的例子

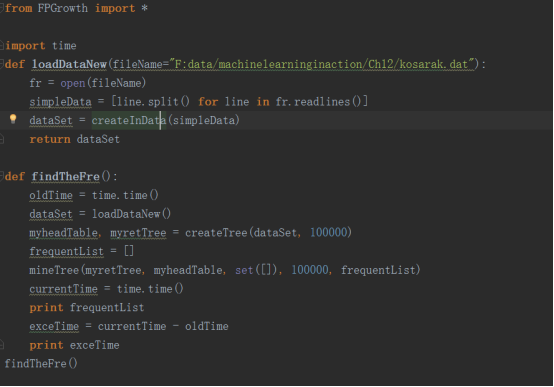
korasa.dat中有100万条数据，我们需要从这一百万条数据中知道最小支持度为100000的频繁项集。如果采用Apriori算法时间非常的长，我等了好几分钟还没出结果，就不等了。

然后采用本节的FP-growth算法只用了11秒多就算完了。以下是具体的代码

六．总结

FP-growth算法作为一种专门发现频繁项集的算法，比Apriori算法的执行效率更高。它只需要扫描数据库两遍，第一遍是为了找到headerTable,也就是找到所有单个的频繁项。第二遍的时候是为了将每一个事务融入到树中。

发现频繁项集是非常有用的操作，经常需要用到，我们可以将其用于搜索，购物交易等多种场景。