动态规划 ---- 最长公共子序列（Longest Common Subsequence, LCS）

分析：

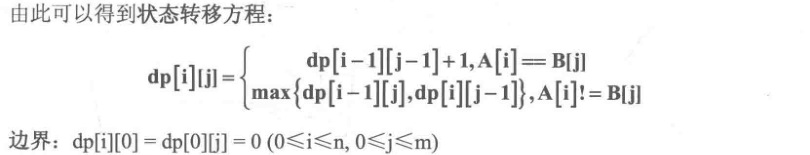
完整代码：

// 最长公共子序列
#include <stdio.h>
#include <algorithm>
using namespace std;

const int N = ;
char A[N], B[N];
int dp[N][N];

int main()
{
    freopen("in.txt", "r", stdin);
    int n;
    gets(A + );        // 从下标1开始读入
    gets(B + );
    int lenA = strlen(A + );    // 由于读入时下标从1开始，因此读取长度也从1开始
    int lenB = strlen(B + );

    // 边界
    for (int i = ; i <= lenA; i++){
        dp[i][] = ;
    }
    for (int j = ; j <= lenB; j++){
        dp[][j] = ;
    }

    // 状态转移方程
    for (int i = ; i <= lenA; i++){
        for (int j = ; j <= lenB; j++){
            if (A[i] == B[j]){
                dp[i][j] = dp[i - ][j - ] + ;
            }
            else{
                dp[i][j] = max(dp[i - ][j], dp[i][j - ]);
            }
        }
    }
    // dp[lenA][lenB]是答案
    printf("%d\n", dp[lenA][lenB]);
    fclose(stdin);
    return ;
}

题型实战：

　　　　　　　　　　　　　　　　1045 Favorite Color Stripe (30分)

Eva is trying to make her own color stripe out of a given one. She would like to keep only her favorite colors in her favorite order by cutting off those unwanted pieces and sewing the remaining parts together to form her favorite color stripe.

It is said that a normal human eye can distinguish about less than 200 different colors, so Eva's favorite colors are limited. However the original stripe could be very long, and Eva would like to have the remaining favorite stripe with the maximum length. So she needs your help to find her the best result.

Note that the solution might not be unique, but you only have to tell her the maximum length. For example, given a stripe of colors {2 2 4 1 5 5 6 3 1 1 5 6}. If Eva's favorite colors are given in her favorite order as {2 3 1 5 6}, then she has 4 possible best solutions {2 2 1 1 1 5 6}, {2 2 1 5 5 5 6}, {2 2 1 5 5 6 6}, and {2 2 3 1 1 5 6}.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤200) which is the total number of colors involved (and hence the colors are numbered from 1 to N). Then the next line starts with a positive integer M (≤200) followed by M Eva's favorite color numbers given in her favorite order. Finally the third line starts with a positive integer L (≤10​4​​) which is the length of the given stripe, followed by L colors on the stripe. All the numbers in a line a separated by a space.

Output Specification:

For each test case, simply print in a line the maximum length of Eva's favorite stripe.

Sample Input:

6
5 2 3 1 5 6
12 2 2 4 1 5 5 6 3 1 1 5 6

Sample Output:

7

分析：

完整代码：

 #include <stdio.h>
 #include <algorithm>
 using namespace std;

 const int maxc = ;        // 颜色的最大种类数
 const int maxn = ;        // 颜色序列的最大长度
 int A[maxc], B[maxn], dp[maxc][maxc];

 int main()
 {
     int n, m;
     scanf("%d%d", &n, &m);
     for (int i = ; i <= m; i++){
         scanf("%d", &A[i]);
     }
     int L;
     scanf("%d", &L);
     for (int i = ; i <= L; i++){
         scanf("%d", &B[i]);
     }
     // 边界
     for (int i = ; i <= m; i++){
         dp[i][] = ;
     }
     for (int j = ; j <= L; j++){
         dp[][j] = ;
     }

     // 状态转移方程
     for (int i = ; i <= m; i++){
         for (int j = ; j <= L; j++){
             // 取dp[i - 1][j]、dp[i][j - 1]中的较大值
             int Max = max(dp[i - ][j], dp[i][j - ]);
             if (A[i] == B[j]){
                 dp[i][j] = Max + ;
             }
             else{
                 dp[i][j] = Max;
             }
         }
     }

     // 输出答案
     printf("%d\n", dp[m][L]);

     return ;
 }