[数据结构]最小生成树算法Prim和Kruskal算法

最小生成树

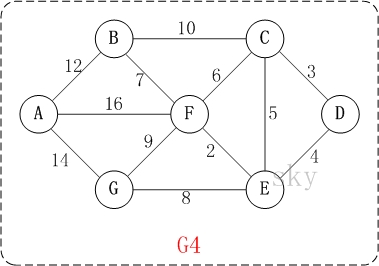
在含有n个顶点的连通图中选择n-1条边，构成一棵极小连通子图，并使该连通子图中n-1条边上权值之和达到最小，则称其为连通网的最小生成树。 

例如，对于如上图G4所示的连通网可以有多棵权值总和不相同的生成树。

普里姆算法介绍

普里姆(Prim)算法，是用来求加权连通图的最小生成树的算法。

基本思想 
对于图G而言，V是所有顶点的集合；现在，设置两个新的集合U和T，其中U用于存放G的最小生成树中的顶点，T存放G的最小生成树中的边。 从所有uЄU，vЄ(V-U) (V-U表示出去U的所有顶点)的边中选取权值最小的边(u, v)，将顶点v加入集合U中，将边(u, v)加入集合T中，如此不断重复，直到U=V为止，最小生成树构造完毕，这时集合T中包含了最小生成树中的所有边。

普里姆算法图解

以上图G4为例，来对普里姆进行演示(从第一个顶点A开始通过普里姆算法生成最小生成树)。

(注：最后一个图画错了，应该是EG)

初始状态：V是所有顶点的集合，即V={A,B,C,D,E,F,G}；U和T都是空！ 
第1步：将顶点A加入到U中。 
    此时，U={A}。 
第2步：将顶点B加入到U中。 
    上一步操作之后，U={A}, V-U={B,C,D,E,F,G}；因此，边(A,B)的权值最小。将顶点B添加到U中；此时，U={A,B}。 
第3步：将顶点F加入到U中。 
    上一步操作之后，U={A,B}, V-U={C,D,E,F,G}；因此，边(B,F)的权值最小。将顶点F添加到U中；此时，U={A,B,F}。 
第4步：将顶点E加入到U中。 
    上一步操作之后，U={A,B,F}, V-U={C,D,E,G}；因此，边(F,E)的权值最小。将顶点E添加到U中；此时，U={A,B,F,E}。 
第5步：将顶点D加入到U中。 
    上一步操作之后，U={A,B,F,E}, V-U={C,D,G}；因此，边(E,D)的权值最小。将顶点D添加到U中；此时，U={A,B,F,E,D}。 
第6步：将顶点C加入到U中。 
    上一步操作之后，U={A,B,F,E,D}, V-U={C,G}；因此，边(D,C)的权值最小。将顶点C添加到U中；此时，U={A,B,F,E,D,C}。 
第7步：将顶点G加入到U中。 
    上一步操作之后，U={A,B,F,E,D,C}, V-U={G}；因此，边(E,G)的权值最小。将顶点G添加到U中；此时，U=V。

此时，最小生成树构造完成！它包括的顶点依次是：A B F E D C G。

克鲁斯卡尔算法介绍

克鲁斯卡尔(Kruskal)算法，是用来求加权连通图的最小生成树的算法。

基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。 
具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。

克鲁斯卡尔算法图解

以上图G4为例，来对克鲁斯卡尔进行演示(假设，用数组R保存最小生成树结果)。

第1步：将边<E,F>加入R中。 
    边<E,F>的权值最小，因此将它加入到最小生成树结果R中。 
第2步：将边<C,D>加入R中。 
    上一步操作之后，边<C,D>的权值最小，因此将它加入到最小生成树结果R中。 
第3步：将边<D,E>加入R中。 
    上一步操作之后，边<D,E>的权值最小，因此将它加入到最小生成树结果R中。 
第4步：将边<B,F>加入R中。 
    上一步操作之后，边<C,E>的权值最小，但<C,E>会和已有的边构成回路；因此，跳过边<C,E>。同理，跳过边<C,F>。将边<B,F>加入到最小生成树结果R中。 
第5步：将边<E,G>加入R中。 
    上一步操作之后，边<E,G>的权值最小，因此将它加入到最小生成树结果R中。 
第6步：将边<A,B>加入R中。 
    上一步操作之后，边<F,G>的权值最小，但<F,G>会和已有的边构成回路；因此，跳过边<F,G>。同理，跳过边<B,C>。将边<A,B>加入到最小生成树结果R中。

此时，最小生成树构造完成！它包括的边依次是：<E,F> <C,D> <D,E> <B,F> <E,G> <A,B>。

克鲁斯卡尔算法分析

根据前面介绍的克鲁斯卡尔算法的基本思想和做法，我们能够了解到，克鲁斯卡尔算法重点需要解决的以下两个问题： 
问题一 对图的所有边按照权值大小进行排序。 
问题二 将边添加到最小生成树中时，怎么样判断是否形成了回路。

问题一很好解决，采用排序算法进行排序即可。

问题二，处理方式是：记录顶点在"最小生成树"中的终点，顶点的终点是"在最小生成树中与它连通的最大顶点"(关于这一点，后面会通过图片给出说明)。然后每次需要将一条边添加到最小生存树时，判断该边的两个顶点的终点是否重合，重合的话则会构成回路。 以下图来进行说明：

在将<E,F> <C,D> <D,E>加入到最小生成树R中之后，这几条边的顶点就都有了终点：

(01) C的终点是F。 
(02) D的终点是F。 
(03) E的终点是F。 
(04) F的终点是F。

关于终点，就是将所有顶点按照从小到大的顺序排列好之后；某个顶点的终点就是"与它连通的最大顶点"。 因此，接下来，虽然<C,E>是权值最小的边。但是C和E的重点都是F，即它们的终点相同，因此，将<C,E>加入最小生成树的话，会形成回路。这就是判断回路的方式。

代码实现

package com.darrenchan.graph;

public class MatrixUDG {

    private int mEdgNum;        // 边的数量
    private char[] mVexs;       // 顶点集合
    private int[][] mMatrix;    // 邻接矩阵
    private static final int INF = Integer.MAX_VALUE;   // 最大值

    /*
     * 创建图(用已提供的矩阵)
     *
     * 参数说明：
     *     vexs  -- 顶点数组
     *     matrix-- 矩阵(数据)
     */
    public MatrixUDG(char[] vexs, int[][] matrix) {

        // 初始化"顶点数"和"边数"
        int vlen = vexs.length;

        // 初始化"顶点"
        mVexs = new char[vlen];
        for (int i = 0; i < mVexs.length; i++)
            mVexs[i] = vexs[i];

        // 初始化"边"
        mMatrix = new int[vlen][vlen];
        for (int i = 0; i < vlen; i++)
            for (int j = 0; j < vlen; j++)
                mMatrix[i][j] = matrix[i][j];

        // 统计"边"
        mEdgNum = 0;
        for (int i = 0; i < vlen; i++)
            for (int j = i+1; j < vlen; j++)
                if (mMatrix[i][j]!=INF)
                    mEdgNum++;
    }

    /*
     * 返回ch位置
     */
    private int getPosition(char ch) {
        for(int i=0; i<mVexs.length; i++)
            if(mVexs[i]==ch)
                return i;
        return -1;
    }

    /*
     * 打印矩阵队列图
     */
    public void print() {
        System.out.printf("Martix Graph:\n");
        for (int i = 0; i < mVexs.length; i++) {
            for (int j = 0; j < mVexs.length; j++)
                System.out.printf("%10d ", mMatrix[i][j]);
            System.out.printf("\n");
        }
    }

    /*
     * prim最小生成树
     *
     * 参数说明：
     *   start -- 从图中的第start个元素开始，生成最小树
     */
    public void prim(int start) {
        int num = mVexs.length;         // 顶点个数
        int index=0;                    // prim最小树的索引，即prims数组的索引
        char[] prims  = new char[num];  // prim最小树的结果数组
        int[] weights = new int[num];   // 顶点间边的权值

        // prim最小生成树中第一个数是"图中第start个顶点"，因为是从start开始的。
        prims[index++] = mVexs[start];

        // 初始化"顶点的权值数组"，
        // 将每个顶点的权值初始化为"第start个顶点"到"该顶点"的权值。
        for (int i = 0; i < num; i++ )
            weights[i] = mMatrix[start][i];
        // 将第start个顶点的权值初始化为0。
        // 可以理解为"第start个顶点到它自身的距离为0"。
        weights[start] = 0;

        for (int i = 0; i < num; i++) {
            // 由于从start开始的，因此不需要再对第start个顶点进行处理。
            if(start == i)
                continue;

            int j = 0;
            int k = 0;
            int min = INF;
            // 在未被加入到最小生成树的顶点中，找出权值最小的顶点。
            while (j < num) {
                // 若weights[j]=0，意味着"第j个节点已经被排序过"(或者说已经加入了最小生成树中)。
                if (weights[j] != 0 && weights[j] < min) {
                    min = weights[j];
                    k = j;
                }
                j++;
            }

            // 经过上面的处理后，在未被加入到最小生成树的顶点中，权值最小的顶点是第k个顶点。
            // 将第k个顶点加入到最小生成树的结果数组中
            prims[index++] = mVexs[k];
            // 将"第k个顶点的权值"标记为0，意味着第k个顶点已经排序过了(或者说已经加入了最小树结果中)。
            weights[k] = 0;
            // 当第k个顶点被加入到最小生成树的结果数组中之后，更新其它顶点的权值。
            for (j = 0 ; j < num; j++) {
                // 当第j个节点没有被处理，并且需要更新时才被更新。
                if (weights[j] != 0 && mMatrix[k][j] < weights[j])
                    weights[j] = mMatrix[k][j];
            }
        }

        // 计算最小生成树的权值
        int sum = 0;
        for (int i = 1; i < index; i++) {
            int min = INF;
            // 获取prims[i]在mMatrix中的位置
            int n = getPosition(prims[i]);
            // 在vexs[0...i]中，找出到j的权值最小的顶点。
            for (int j = 0; j < i; j++) {
                int m = getPosition(prims[j]);
                if (mMatrix[m][n]<min)
                    min = mMatrix[m][n];
            }
            sum += min;
        }
        // 打印最小生成树
        System.out.printf("PRIM(%c)=%d: ", mVexs[start], sum);
        for (int i = 0; i < index; i++)
            System.out.printf("%c ", prims[i]);
        System.out.printf("\n");
    }

    /*
     * 克鲁斯卡尔（Kruskal)最小生成树
     */
    public void kruskal() {
        int index = 0;                      // rets数组的索引
        int[] vends = new int[mEdgNum];     // 用于保存"已有最小生成树"中每个顶点在该最小树中的终点。
        EData[] rets = new EData[mEdgNum];  // 结果数组，保存kruskal最小生成树的边
        EData[] edges;                      // 图对应的所有边

        // 获取"图中所有的边"
        edges = getEdges();
        // 将边按照"权"的大小进行排序(从小到大)
        sortEdges(edges, mEdgNum);

        for (int i=0; i<mEdgNum; i++) {
            int p1 = getPosition(edges[i].start);      // 获取第i条边的"起点"的序号
            int p2 = getPosition(edges[i].end);        // 获取第i条边的"终点"的序号

            int m = getEnd(vends, p1);                 // 获取p1在"已有的最小生成树"中的终点
            int n = getEnd(vends, p2);                 // 获取p2在"已有的最小生成树"中的终点
            // 如果m!=n，意味着"边i"与"已经添加到最小生成树中的顶点"没有形成环路
            if (m != n) {
                vends[m] = n;                       // 设置m在"已有的最小生成树"中的终点为n
                rets[index++] = edges[i];           // 保存结果
            }
        }

        // 统计并打印"kruskal最小生成树"的信息
        int length = 0;
        for (int i = 0; i < index; i++)
            length += rets[i].weight;
        System.out.printf("Kruskal=%d: ", length);
        for (int i = 0; i < index; i++)
            System.out.printf("(%c,%c) ", rets[i].start, rets[i].end);
        System.out.printf("\n");
    }

    /*
     * 获取图中的边
     */
    private EData[] getEdges() {
        int index=0;
        EData[] edges;

        edges = new EData[mEdgNum];
        for (int i=0; i < mVexs.length; i++) {
            for (int j=i+1; j < mVexs.length; j++) {
                if (mMatrix[i][j]!=INF) {
                    edges[index++] = new EData(mVexs[i], mVexs[j], mMatrix[i][j]);
                }
            }
        }

        return edges;
    }

    /*
     * 对边按照权值大小进行排序(由小到大)
     */
    private void sortEdges(EData[] edges, int elen) {

        for (int i=0; i<elen; i++) {
            for (int j=i+1; j<elen; j++) {

                if (edges[i].weight > edges[j].weight) {
                    // 交换"边i"和"边j"
                    EData tmp = edges[i];
                    edges[i] = edges[j];
                    edges[j] = tmp;
                }
            }
        }
    }

    /*
     * 获取i的终点
     */
    private int getEnd(int[] vends, int i) {
        while (vends[i] != 0)
            i = vends[i];
        return i;
    }

    // 边的结构体
    private static class EData {
        char start; // 边的起点
        char end;   // 边的终点
        int weight; // 边的权重

        public EData(char start, char end, int weight) {
            this.start = start;
            this.end = end;
            this.weight = weight;
        }
    };

    public static void main(String[] args) {
        char[] vexs = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
        int matrix[][] = {
                /*A*//*B*//*C*//*D*//*E*//*F*//*G*/
                /*A*/ {   0,  12, INF, INF, INF,  16,  14},
                /*B*/ {  12,   0,  10, INF, INF,   7, INF},
                /*C*/ { INF,  10,   0,   3,   5,   6, INF},
                /*D*/ { INF, INF,   3,   0,   4, INF, INF},
                /*E*/ { INF, INF,   5,   4,   0,   2,   8},
                /*F*/ {  16,   7,   6, INF,   2,   0,   9},
                /*G*/ {  14, INF, INF, INF,   8,   9,   0}};
        MatrixUDG pG;

        // 采用已有的"图"
        pG = new MatrixUDG(vexs, matrix);

        //pG.print();   // 打印图
        pG.prim(0);   // prim算法生成最小生成树
        pG.kruskal();   // Kruskal算法生成最小生成树
    }
}

参考：

https://www.cnblogs.com/skywang12345/p/3711510.html

https://www.cnblogs.com/skywang12345/p/3711504.html

https://blog.csdn.net/CmdSmith/article/details/56274314

https://blog.csdn.net/CmdSmith/article/details/56288430

https://blog.csdn.net/zfyseu1/article/details/54973572