HGOI 20181101题解
/*
又是爆0的一天(不知道今年高考难不难,反正今天(信息学)真的难!)
*/

solution:对于两个数相加,有一个显然的结论就是要么不进位(相对于位数大的),要么(进最多一位)
然后对于整个数组先排序,然后枚举每一个数,在它的前面找到和他相加进1位的点,讨论不变位和进一位累加求和即可
由于数列有序对于最左边的p满足f(a[p]+a[now])=f(a[now])+1对于他的右边所有的数都符合进一位的条件,这样可以二分查找找到最左端的点
# pragma GCC optimze()
# include<bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=1e6+;
int n,a[MAXN];
inline int read()
{
int X=,w=;char c=;
while (!(c>=''&&c<='')) w|=c=='-',c=getchar();
while (c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
return w?-X:X;
}
int fun(int x)
{
int ret=;
while (x){ ret++; x/=;}
return ret;
}
int find(int sl,int sr,int id)
{
int l=sl,r=sr,ans=-;
int tmp=fun(a[id])+;
while (l<=r) {
int mid=(l+r)/;
if (fun(a[mid]+a[id])==tmp) r=mid-,ans=mid;
else l=mid+;
}
return ans;
}
signed main()
{
n=read();
for (int i=;i<=n;i++) a[i]=read();
sort(a+,a++n);
int ans=;
for (int i=;i<=n;i++) {
int p=find(,i-,i),tmp=fun(a[i]);
if (p==-) ans+=tmp*(i-);
else ans+=(tmp+)*(i-p)+tmp*(p-);
}
cout<<ans<<endl;
return ;
}

solution:这个题有一个结论,就是对于全集U={所有人}的2n个子集,存在tot个满足下面关系的子集
子集中所有的权重加起来不足m,但是从其他不选的人随便拿一个放入子集权重都能大于等于m,最终统计出的tot就是答案
也就是最少需要锁的个数。
上面的结论是我们构造出来的,然后我们需要证明这个结论。
现在首先是两个性质的事情,
数学上我们定义:
- 证明条件:通过所有的证明条件推出一个结论的条件全集。
- 必要条件:是证明条件的子集,所有的必要条件的全集就是证明条件,无论是什么证明方法,都需要的条件。
- 充分条件:证明条件是充分条件的子集,也就是满足充分条件的一定满足必要条件。
(如证明一个图形是直角三角形,必要条件可以是:这个图形是三角形,充分条件可以是:这个图形是等腰RT三角形)
有这样的结论:
- 所有有这样的关系:必要条件⊆证明条件⊆充分条件
- 如果一个条件集既是必要条件又是充分条件,那么这个条件必然是证明条件。
- 我们证明必要条件就是证明满足这样的条件不一定可以构造出合法答案(找到反例)
- 我们证明充分条件就是在充分条件下,构造一种方法让其条件合法
回到题目,我们来证明上面的必要性和充分性,
- 必要性:由于上面任一子集的权值和都不足m,那么他们都至少缺一把锁不能开启,若锁的个数不足所有合法子集数把锁,那么由鸽巢原理可知,必然有两个子集缺的是同一把锁,然后如果我们把这两个子集拼起来,那么他们的权值和已经大于m了却不能打开全部的锁,与题意矛盾,故证明必要性。(可知锁至少是tot个)
- 充分性:(如果锁恰好是tot那么一定存在一种合法的分配方式让他们满足题设)假设我们将每一把锁(tot个)上都写一个居民的子集,然后令一个居民拥有除了这个居民对应的一把钥匙,然后任取一个集合和这个居民配对显然可以开启所有的锁,所有其充分性得证。
- 所以我们提出的条件是充分必要条件,所有就是证明条件,证必。
# include <bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=;
int a[MAXN],t[MAXN];
int ans,n,m;
bool check()
{
int sum=;
for (int i=;i<=n;i++) if (t[i]) sum+=a[i];
if (sum>=m) return false;
for (int i=;i<=n;i++)
if (t[i]==&&sum+a[i]<m) return false;
return true;
}
void dfs(int dep)
{
if (dep==n+) { if (check()) ans++; return;}
t[dep]=;dfs(dep+);
t[dep]=;dfs(dep+);
}
signed main()
{
scanf("%d%d",&n,&m);
for (int i=;i<=n;i++) scanf("%d",&a[i]);
memset(t,,sizeof(t));
ans=;
dfs();
cout<<ans<<endl;
return ;
}

solution:
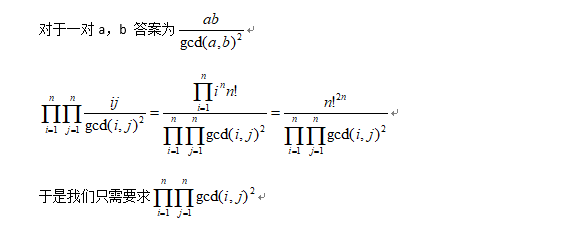



HGOI 20181101题解的更多相关文章
- HGOI 20181028 题解
HGOI 20181028(复赛备考) /* 真是暴力的一天,最后一题MLE?由于数组开得太大了!!! 270滚粗 考场上好像智商高了很多?!(假的) */ sol:暴力求解,然后没有数据范围吐槽一下 ...
- HGOI 20190310 题解
/* 又是又双叒叕WA的一天... 我太弱鸡了... 今天上午打了4道CF */ Problem 1 meaning 给出q组询问,求下列函数的值$ f(a) = \max\limits_{0 < ...
- HGOI 20190303 题解
/* 记一串数字真难. 5435 今天比赛又是hjcAK的一天. 今天开题顺序是312,在搞T1之前搞了T3 昨天某谷月赛真是毒瘤. 但是讲评的同学不错,起码T4看懂了... 构造最优状态然后DP的思 ...
- HGOI 20180224 题解
/* The Most Important Things: ljc chat with fyh on QQTa说期末考Ta数学74分感觉不好但是我觉得fyh是地表最强的鸭~~(of course en ...
- HGOI 20190218 题解
/* 又是AK局... hjc又双叒叕AK了... Hmmm...我侥幸 */ Problem A card 给出无序序列a[]可以选择一个数插入到合适的位置作为一次操作,至少多少次操作后可以把序列变 ...
- HGOI 20190217 题解
/* for me,开训第一天 /beacuse 文化课太差被抓去补文化课了... 看一眼题 : AK局? 但是,Wa on test #10 in problem C 290! (就差那么一咪咪) ...
- HGOI 20181103 题解
problem:把一个可重集分成两个互异的不为空集合,两个集合里面的数相乘的gcd为1(将集合中所有元素的质因数没有交集) solution:显然本题并不是那么容易啊!考场上想了好久.. 其实转化为上 ...
- HGOI 20191108 题解
Problem A 新婚快乐 一条路,被$n$个红绿灯划分成$n+1$段,从前到后一次给出每一段的长度$l_i$,每走$1$的长度需要$1$分钟. 一开始所有红绿灯都是绿色的,$g$分钟后所有红绿灯变 ...
- HGOI 20191107 题解
Problem A 树状数组 给出下列$C++$代码: 设区间加操作$modify(l,r)$为调用两次$update(r,1)$和$update(l-1,-1)$ 设$f(l,r)$表示在初始$cn ...
随机推荐
- HDU2552 三足鼎立 【数学推理】
三足鼎立 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submi ...
- 大数据入门第十四天——Hbase详解(一)入门与安装配置
一.概述 1.什么是Hbase 根据官网:https://hbase.apache.org/ Apache HBase™ is the Hadoop database, a distributed, ...
- 2017-2018-2 20155203《网络对抗技术》Exp2 后门原理与实践
基础问题回答 (1)例举你能想到的一个后门进入到你系统中的可能方式? 通过下载带后门的程序或者点开带有后门的软件,或者后门本身就在我的系统里: (2)例举你知道的后门如何启动起来(win及linux) ...
- 20155321 《网络攻防》 Exp8 Web基础
20155321 <网络攻防> Exp8 Web基础 基础问题回答 什么是表单? 表单是主要负责数据采集功能.主要是以下三个部分构成: 表单标签:包含处理表单数据所用的程序的URL以及数据 ...
- Dynamics CRM2016 导入数据格式之xlsx的应用
在CRM中导入数据中新增加了一个xlsx格式,这个在之前的版本(2013中没有,2015不清楚是否有)中是没有的 本篇的目的就是为了提醒各位,不要把这个格式和csv的导入功能混淆,因为xlsx格式的用 ...
- [穷尽]ADO.NET连接字符串
微软提供的四种数据库连接方式: System.Data.OleDb.OleDbConnection System.Data.SqlClient.SqlConnection System.Data.Od ...
- effective c++ 笔记 (30-31)
//---------------------------15/04/17---------------------------- //#30 透彻了解inlineing的里里外外 { /* 1: ...
- 使用unity3d和tensorflow实现基于姿态估计的体感游戏
使用unity3d和tensorflow实现基于姿态估计的体感游戏 前言 之前做姿态识别,梦想着以后可以自己做出一款体感游戏,然而后来才发现too young.但是梦想还是要有的,万一实现了呢.趁着p ...
- 《Pro SQL Server Internals, 2nd edition》中CHAPTER 7 Designing and Tuning the Indexes中的Clustered Index Design Considerations一节(译)
<Pro SQL Server Internals> 作者: Dmitri Korotkevitch 出版社: Apress出版年: 2016-12-29页数: 804定价: USD 59 ...
- webstorm开发微信小程序代码提醒(webstorm开发工具)
使用了微信提供的开发工具是真心难用,卡顿厉害.中英文切写注释换相当不爽.还没办法多开窗口,相信大家也遇到过这种现象. 下边我们介绍下webstorm来开发微信小程序的一些配置: File---sett ...
