Python实现迪杰斯特拉算法

首先我采用邻接矩阵法来表示图（有向图无向图皆可）

图的定义如下:

class Graph:
    def __init__(self, arcs=[]):
        self.vexs = []
        self.arcs = arcs

    def creategrapg(self):
        self.vexs = input().split()
        for i in range(len(self.vexs)):
            self.arcs.append([float('inf') if int(v) == 0 else int(v)
                              for v in input().split()])

其中creategrapg用来创建图，创建图时，首先输入所有顶点，以空格分隔在一行内输入，后面为一个n*n的矩阵，n为顶点数目。

算法具体实现如下：

    def ShortestPath_DIJ(self, v):
        #迪杰斯特拉算法
        v0 = self.vexs.index(v)
        n = len(self.vexs)
        S = [False] * n
        S[v0] = True
        D = self.arcs[v0].copy()
        Path = [-1] * n
        for i in range(n):
            if D[i] < float('inf'):
                Path[i] = v0
        D[v0] = 0
        for i in range(1, n):
            min_ = float('inf')
            for w in range(n):
                if not S[w] and D[w] < min_:
                    v_ = w
                    min_ = D[w]
            S[v_] = True
            for w in range(n):
                if not S[w] and (D[v_] + self.arcs[v_][w] < D[w]):
                    D[w] = D[v_] + self.arcs[v_][w]
                    Path[w] = v_
        print(f'从{v}到各顶点的最短路径为:')
        # 算法到此其实已经结束，下面我自己写的用来展示路径的部分
        for ind, val in enumerate(Path):
            if ind == v0:
                continue
            if val == -1:
                print(f'{self.vexs[ind]}:不可到达')
                continue
            path_ = [self.vexs[ind]]
            while val > 0:
                path_.append(self.vexs[val])
                val = Path[val]
            # path_.append(v)
            print(self.vexs[ind] + ':' + '->'.join(path_[::-1]))

注：这个函数实际上是写在Graph类里面的，为了方便叙述我才分开放了代码。

运行代码：

mygraph = Graph()
mygraph.creategrapg()
mygraph.ShortestPath_DIJ(mygraph.vexs[1])

输入的图如下图所示。

输入样例为：

v0 v1 v2 v3 v4 v5
0 0 10 0 30 100
0 0 5 0 0 0
0 0 0 50 0 0
0 0 0 20 0 10
0 0 0 0 0 60
0 0 0 0 0 0

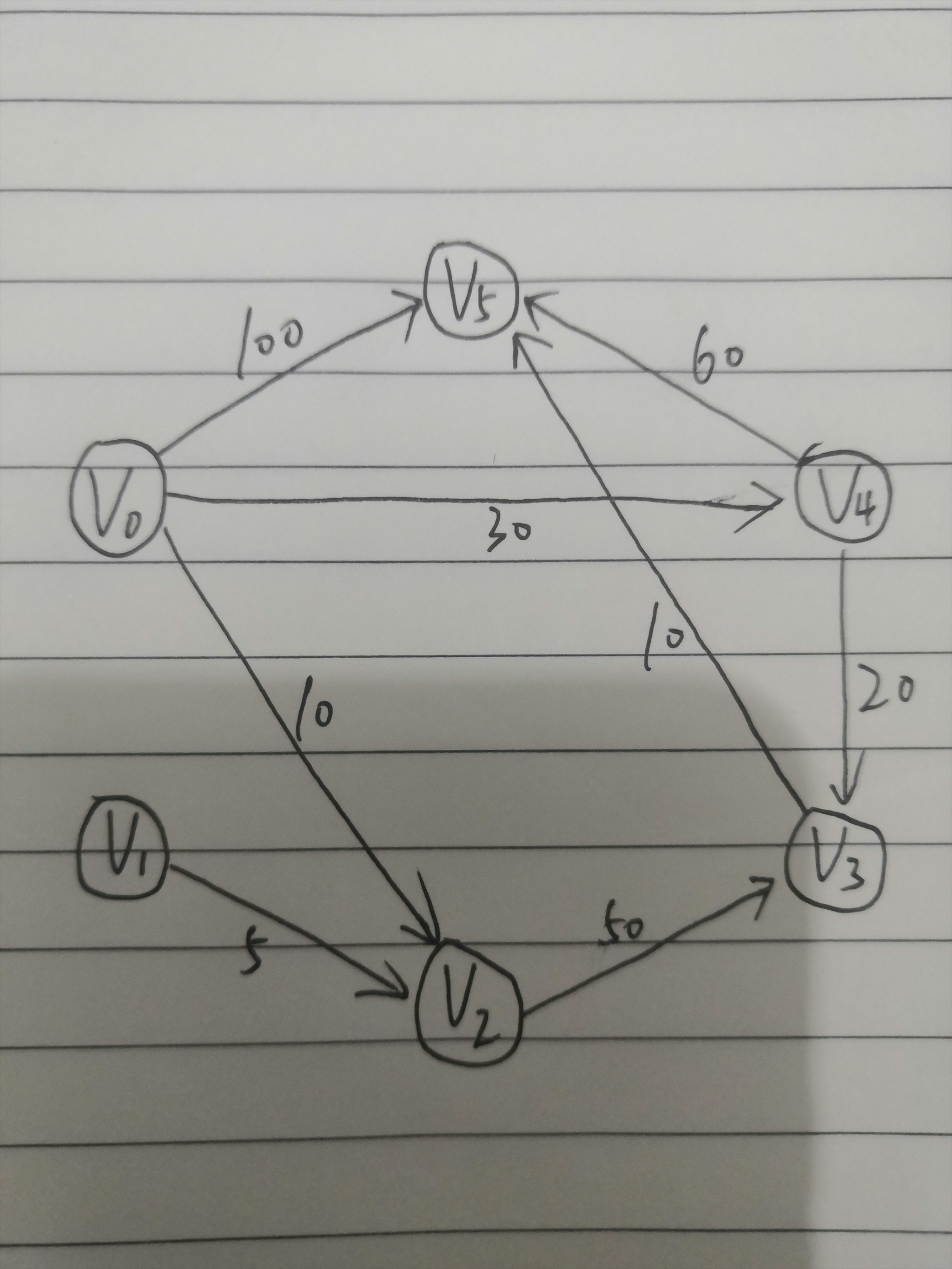
运行结果如下：

从v1到各顶点的最短路径为:
v0:不可到达
v2:v1->v2
v3:v1->v2->v3
v4:不可到达
v5:v1->v2->v3->v5