BZOJ1001 狼抓兔子（网络流转最短路：对偶图）

题意：

给一个如图形式的\(n*m\)的方格，从左上走到右下，给出边权，问分成两块所需的最小代价。\(n,m\leq1000\)。

思路：

显然是个最小割，但是\(O(n^2m)\)的复杂度很高，虽然这道题能过。

这里介绍一种最大流改最短路的方法——对偶图。

对任意一个图我们可以变成对偶图：

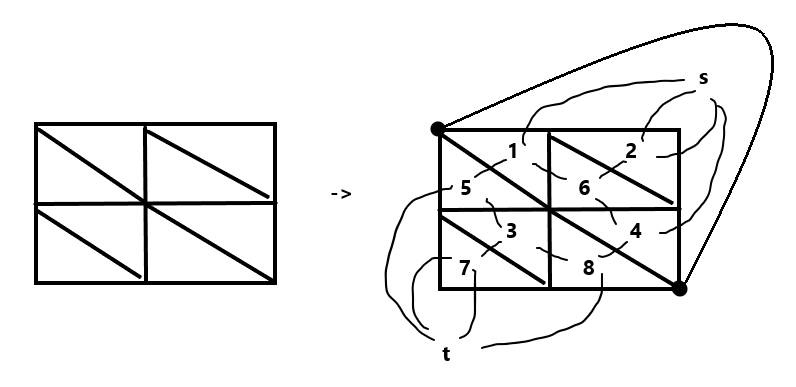
如下图，每一个闭合的平面我们都给他标号，然后连接源点和汇点，把外面那个无穷大的平面分成两个平面\(s,t\)。然后开始新建边。新建边的每一条边为：把一条原来边的左右两个平面连接到一起，权值为原来的边的权值。可以得出最后的新建的边的数量和原来一样。最后跑\(s,t\)的最短路即可得出原图的最大流。

代码：

#include <map>
#include <set>
#include <queue>
#include <cmath>
#include <stack>
#include <ctime>
#include <vector>
#include <cstdio>
#include <string>
#include <cstring>
#include <sstream>
#include <iostream>
#include <algorithm>
typedef long long ll;
typedef unsigned long long ull;
using namespace std;
const int maxn = 3e6 + 5;
const int MAXM = 3e6;
const ll MOD = 1e9 + 7;
const ull seed = 131;
const int INF = 0x3f3f3f3f;
struct Edge{
    int to, next;
    int w;
}edge[MAXM * 2];
struct qnode{
    int u;
    int c;
    qnode(int _u = 0, int _c = 0):u(_u), c(_c){}
    bool operator < (const qnode &r) const{
        return r.c < c;
    }
};
int tot, head[maxn], vis[maxn];
int dis[maxn];
void addEdge(int u, int v, int w){
    edge[tot].to = v;
    edge[tot].w = w;
    edge[tot].next = head[u];
    head[u] = tot++;
}
void Dijkstra(int n, int st){
    memset(vis, 0, sizeof(vis));
    for(int i = 0; i <= n; i++) dis[i] = INF;
    priority_queue<qnode> que;
    while(!que.empty()) que.pop();
    dis[st] = 0;
    que.push(qnode(st, 0));
    qnode temp;
    while(!que.empty()){
        temp = que.top();
        que.pop();
        int u = temp.u;
        if(vis[u]) continue;
        vis[u] = 1;
        for(int i = head[u]; i != -1; i = edge[i].next){
            int v = edge[i].to;
            int w = edge[i].w;
            if(!vis[v] && dis[v] > dis[u] + w){
                dis[v] = dis[u] + w;
                que.push(qnode(v, dis[v]));
            }
        }
    }
}
int n, m;
int getupid(int x, int y){
    return (x - 1) * (m - 1) + y;
}
int getdownid(int x, int y){
    return (x - 1) * (m - 1) + y + (n - 1) * (m - 1);
}
int main(){
    memset(head, -1, sizeof(head));
    tot = 0;
    scanf("%d%d", &n, &m);
    if(n == 1 || m == 1){
        int ans = INF;
        if(n == m) ans = 0;
        if(n < m) swap(n, m);
        for(int i = 1; i <= n - 1; i++){
            int w;
            scanf("%d", &w);
            ans = min(ans, w);
        }
        printf("%d\n", ans);
        return 0;
    }
    int st = 0, en = (n - 1) * (m - 1) * 2 + 1;
    for(int i = 1; i <= n; i++){
        for(int j = 1; j <= m - 1; j++){
            int w;
            scanf("%d", &w);
            if(i == 1){
                addEdge(st, getupid(i, j), w);
                addEdge(getupid(i, j), st, w);
            }
            else if(i == n){
                addEdge(en, getdownid(i - 1, j), w);
                addEdge(getdownid(i - 1, j), en, w);
            }
            else{
                addEdge(getupid(i, j), getdownid(i - 1, j), w);
                addEdge(getdownid(i - 1, j), getupid(i, j), w);
            }
        }
    }

    for(int i = 1; i <= n - 1; i++){
        for(int j = 1; j <= m; j++){
            int w;
            scanf("%d", &w);
            if(j == 1){
                addEdge(getdownid(i, j), en, w);
                addEdge(en, getdownid(i, j), w);
            }
            else if(j == m){
                addEdge(getupid(i, j - 1), st, w);
                addEdge(st, getupid(i, j - 1), w);
            }
            else{
                addEdge(getdownid(i, j), getupid(i, j - 1), w);
                addEdge(getupid(i, j - 1), getdownid(i, j), w);
            }
        }
    }

    for(int i = 1; i <= n - 1; i++){
        for(int j = 1; j <= m - 1; j++){
            int w;
            scanf("%d", &w);
            addEdge(getupid(i, j), getdownid(i, j), w);
            addEdge(getdownid(i, j), getupid(i, j), w);
        }
    }

    Dijkstra(en, st);
    printf("%d\n", dis[en]);

    return 0;
}