SparkMLlib学习之线性回归

SparkMLlib学习之线性回归

（一）回归的概念

　　1，回归与分类的区别

　　　分类模型处理表示类别的离散变量，而回归模型则处理可以取任意实数的目标变量。但是二者基本的原则类似，都是通过确定一个模型，将输入特征映射到预测的输出。回归模型和分类模型都是监督学习的一种形式。

　　2.回归分类

　　　线性回归模型：本质上和对应的线性分类模型一样，唯一的区别是线性回归使用的损失函数、相关连接函数和决策函数不同。MLlib提供了标准的最小二乘回归模型在MLlib中，标准的最小二乘回归不使用正则化。但是应用到错误预测值的损失函数会将错误做平方，从而放大损失。这也意味着最小平方回归对数据中的异常点和过拟合非常敏感。因此对于分类器，我们通常在实际中必须应用一定程度的正则化。正则化分为：应用L2正则化时通常称为岭回归（ridge regression），应用L1正则化是称为LASSO（Least Absolute Shrinkage and Selection Operator）。

　　　决策树模型：决策树同样可以通过改变不纯度的度量方法用于回归分析

（二）SparkMLlib线性回归的应用

　　1，数据集的选择

　　　　http://archive.ics.uci.edu/ml/datasets/Bike+Sharing+Dataset。

　　2.数据集的描述

　　　　此数据是根据一系列的特征预测每小时自行车租车次数，特征类型如下：

　　3，数据处理及构建模型

　　　　数据集中共有17 379个小时的记录。接下来的实验，我们会忽略记录中的 instant和 dteday 。忽略两个记录次数的变量 casual 和 registered ，只保留 cnt （ casual 和registered 的和）。最后就剩下12个变量，其中前8个是类型变量，后4个是归一化后的实数变量。对其中8个类型变量，我们使用之前提到的二元编码，剩下4个实数变量不做处理。另外一种二元变量化方法：http://blog.csdn.net/u010824591/article/details/50374904

import org.apache.log4j.{Level, Logger}
import org.apache.spark.mllib.linalg.Vectors
import org.apache.spark.mllib.regression.{LabeledPoint, LinearRegressionWithSGD}
import org.apache.spark.mllib.tree.DecisionTree
import org.apache.spark.rdd.RDD
import org.apache.spark.{SparkConf, SparkContext}

/**
  * Created by Damon on 17-5-22.
  */
object Regression {
  def main(args: Array[String]): Unit = {
    Logger.getLogger("org.apache.spark").setLevel(Level.WARN)
    Logger.getLogger("org.eclipse.jetty.server").setLevel(Level.OFF)
    val conf =new SparkConf().setAppName("regression").setMaster("local[4]")
    val sc =new SparkContext(conf)
    //文件名
    val file_bike="hour_nohead.csv"
    //调用二元向量化方法
    val labeled_file=labeledFile(file_bike,sc)
    /*/*对目标值取对数*/
    val labeled_file1=labeled_file.map(point => LabeledPoint(math.log(point.label),point.features))
    */
    //构建线性回归模型，注该方法在：spark2.1.0已经抛弃了。。。。
    val model_liner=LinearRegressionWithSGD.train(labeled_file,10,0.1)
    //val categoricalFeaturesInfo = Map[Int,Int]()
    //val model_DT=DecisionTree.trainRegressor(labeled_file,categoricalFeaturesInfo,"variance",5,32)
    val predict_vs_train=labeled_file.map{
      point => (model_liner.predict(point.features),point.label)
//对目标取对数后的，预测方法
     /* point => (math.exp(model_liner.predict(point.features)),math.exp(point.label))*/
    }
    predict_vs_train.take(5).foreach(println(_))
   /*
(135.94648455498356,16.0)
(134.38058174607252,40.0)
(134.1840793861374,32.0)
(133.88699144084515,13.0)
(133.77899037657548,1.0)
   */
  def labeledFile(originFile:String,sc:SparkContext):RDD[LabeledPoint]={
    val file_load=sc.textFile(originFile)
    val file_split=file_load.map(_.split(","))
    /*构建映射类函数的方法:mapping*/
    def mapping(rdd:RDD[Array[String]],index:Int)=
      rdd.map(x => x(index)).distinct.zipWithIndex().collect.toMap
    /*存储每列映射方法mapping的maps集合*/
    var maps:Map[Int,Map[String,Long]] = Map()
    /* 生成maps*/
    for(i <- 2 until 10)
      maps += (i -> mapping(file_split,i))
    /*max_size表示每列的特征之和*/
    val max_size=maps.map(x =>x._2.size).sum
    val file_label=file_split.map{
      x =>
        var num:Int=0
        var size:Int=0
        /*构建长度为max_size+4的特征数组,初始值全为0*/
        val arrayOfDim=Array.ofDim[Double](max_size+4)
        for(j<-2 until 10) {
          num = maps(j)(x(j)).toInt
          if(j==2) size=0 else size += maps(j-1).size
          /*为特征赋值*/
          arrayOfDim(size+num)=1.0
        }
        /*添加后面4列归一化的特征*/
        for(j<-10 until 14)
        arrayOfDim(max_size+(j-10))=x(j).toDouble
        /*生成LabeledPoint类型*/
        LabeledPoint(x(14).toDouble+x(15).toDouble,Vectors.dense(arrayOfDim))
    }
    file_label
  }
}

　　4，模型性能评价

　　　　(1) MSE是均方误差，是用作最小二乘回归的损失函数，表示所有样本预测值和实际值平方差的平均值。公式如下：

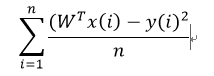
　　　　(2)RMSE是MSE的平方根　　　　

　　　　(3)平均绝对误差（MAE）：预测值与实际值的绝对值差的平均值

　　　　　　　　　　　　

　　　　(4) 均方根对数误差（RMSLE）：预测值和目标值进行对数变换后的RMSE.

代码如下：

/*MSE是均方误差*/
    val mse=predict_vs_train.map(x => math.pow(x._1-x._2,2)).mean()
   /* 平均绝对误差（MAE）*/
    val mae=predict_vs_train.map(x => math.abs(x._1-x._2)).mean()
    /*均方根对数误差（RMSLE）*/
    val rmsle=math.sqrt(predict_vs_train.map(x => math.pow(math.log(x._1+1)-math.log(x._2+1),2)).mean())
    println(s"mse is $mse and mae is $mae and rmsle is $rmsle")
/*
mse is 29897.34020145107 and mae is 130.53255991178477 and rmsle is 1.4803867063174845
*/

（三） 改进模型性能和参数调优

　　1，变换目标变量

　　　许多机器学习模型都会假设输入数据和目标变量的分布，比如线性模型的假设为正态分布，这里就将目标值取对数（还可以去sqrt处理）（将上文注释去掉）实现正态分布，结果如为：mse is 47024.572159822106 and mae is 149.28861881845546 and rmsle is 1.4525632598540426

　　将上述结果和原始数据训练的模型性能比较，可以看到我们提升了RMSLE的性能，但是却没有提升MSE和MAE的性能。

　　2.交叉验证

　　　1，创建训练集和测试集来评估参数

　　　2，调节参数来判断对线性模型的影响

迭代次数及步长的影响：

//划分训练集和测试集
    val labeled_orign = labeled_file.randomSplit(Array(0.8, 0.2), 11L)
    val train_file = labeled_orign()
    val test_file = labeled_orign()
    /*调节迭代次数*/
    val Iter_Results = Seq(, , , , , ).map { param =>
      val model = LinearRegressionWithSGD.train(test_file, param, 0.01)
      val scoreAndLabels = test_file.map { point =>
        (model.predict(point.features), point.label)
      }
      val rmsle = math.sqrt(scoreAndLabels.map(x => math.pow(math.log(x._1) - math.log(x._2), )).mean)
      (s"$param lambda", rmsle)
    }
    /*迭代次数的结果输出*/
    Iter_Results.foreach { case (param, rmsl) => println(f"$param, rmsle = ${rmsl}")}
    /*调节步长数的大小*/
    val Step_Results = Seq(0.01, 0.025, 0.05, 0.1, 1.0).map { param =>
        val model = LinearRegressionWithSGD.train(test_file, , param)
        val scoreAndLabels = test_file.map { point =>
          (model.predict(point.features), point.label)
        }
        val rmsle = math.sqrt(scoreAndLabels.map(x => math.pow(math.log(x._1) - math.log(x._2), )).mean)
        (s"$param lambda", rmsle)
      }
    /*步长的结果输出*/
    Step_Results.foreach { case (param, rmsl) => println(f"$param, rmsle = ${rmsl}")}
/*results
1 lambda, rmsle = 2.9033629718241167
5 lambda, rmsle = 2.0102924520366092
10 lambda, rmsle = 1.7548482896314488
20 lambda, rmsle = 1.5785106813100764
50 lambda, rmsle = 1.461748782192306
100 lambda, rmsle = 1.4462810196387068
步长
0.01 lambda, rmsle = 1.5785106813100764
0.025 lambda, rmsle = 1.4478358250917658
0.05 lambda, rmsle = 1.5152549319928832
0.1 lambda, rmsle = 1.5687431700715837
1.0 lambda, rmsle = NaN
*/

　　结果表明，随着迭代次数的增加，误差确实有所下降（即性能提高），并且下降速率和预期一样越来越小。可以看出为什么不使用默认步长来训练线性模型。其中默认步长为1.0，得到的RMSLE结果为 nan 。这说明SGD模型收敛到了最差的局部最优解。这种情况在步长较大的时候容易出现，原因是算法收敛太快而不能得到最优解。另外，小步长与相对较小的迭代次数（比如上面的10次）对应的训练模型性能一般较差。而较小的步长与较大的迭代次数下通常可以收敛得到较好的解。通常来讲，步长和迭代次数的设定需要权衡。较小的步长意味着收敛速度慢，需要较大的迭代次数。但是较大的迭代次数更加耗时，特别是在大数据集上。

　　还可以调节L1正则化和L2正则化参数。 MLlib目前支持两种正则化方法L1和L2。 L2正则化假设模型参数服从高斯分布，L2正则化函数比L1更光滑，所以更容易计算；L1假设模型参数服从拉普拉斯分布，L1正则化具备产生稀疏解的功能，从而具备Feature Selection的能力。（由于spark 2.1.0中的线性回归方法已经忽略了，就没去验证L1和L2对模型的影响）