L1正则是权值的绝对值之和，重点在于可以稀疏化，使得部分权值等于零。

L1正则的含义是 ∥w∥≤c，如下图就可以解释为什么会出现权值为零的情况。

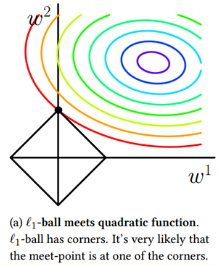
L1正则在梯度下降的时候不可以直接求导，可以有以下几种方法来优化

1.OWL-QN算法http://blog.csdn.net/google19890102/article/details/47424845

对于目标函数中包含加性的非平滑项并使用梯度下降求解的问题，如果可以使用proximal operator，则解法如下：

假设目标函数为 其中 可导，而 不可导。
则每步迭代更新为
其中，
如果 ，也就是题目中要求的L1范数正则化，则对应的

 2.在scikit-learn中l1正则使用坐标下降和最小角回归来实现优化的

坐标轴下降是每次固定其他维度，选择其中一个维度来更新目标函数值，遍历所有的维度，迭代多次，直到目标函数值没有发生明显变化。

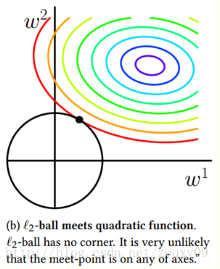
L2正则的重点在于防止过拟合，没有稀疏特征的效果。L2正则在梯度下降的时候可以直接求导

∥w∥2≤c

L1正则与L2正则的更多相关文章

  1. 【机器学习】--鲁棒性调优之L1正则，L2正则

    一.前述 鲁棒性调优就是让模型有更好的泛化能力和推广力. 二.具体原理 1.背景 第一个更好,因为当把测试集带入到这个模型里去.如果测试集本来是100,带入的时候变成101,则第二个模型结果偏差很大, ...

  2. 【机器学习】--线性回归中L1正则和L2正则

    一.前述 L1正则,L2正则的出现原因是为了推广模型的泛化能力.相当于一个惩罚系数. 二.原理 L1正则:Lasso Regression L2正则:Ridge Regression 总结: 经验值 ...

  3. 贝叶斯先验解释l1正则和l2正则区别

    这里讨论机器学习中L1正则和L2正则的区别. 在线性回归中我们最终的loss function如下: 那么如果我们为w增加一个高斯先验,假设这个先验分布是协方差为 的零均值高斯先验.我们在进行最大似然 ...

  4. L1 正则 和 L2 正则的区别

    L1,L2正则都可以看成是 条件限制,即 $\Vert w \Vert \leq c$ $\Vert w \Vert^2 \leq c$ 当w为2维向量时,可以看到,它们限定的取值范围如下图: 所以它 ...

  5. L1正则和L2正则的比较分析详解

    原文链接:https://blog.csdn.net/w5688414/article/details/78046960 范数(norm) 数学上,范数是一个向量空间或矩阵上所有向量的长度和大小的求和 ...

  6. 大白话5分钟带你走进人工智能-第十五节L1和L2正则几何解释和Ridge，Lasso，Elastic Net回归

    第十五节L1和L2正则几何解释和Ridge,Lasso,Elastic Net回归 上一节中我们讲解了L1和L2正则的概念,知道了L1和L2都会使不重要的维度权重下降得多,重要的维度权重下降得少,引入 ...

  7. 大白话5分钟带你走进人工智能-第十四节过拟合解决手段L1和L2正则

                                                                               第十四节过拟合解决手段L1和L2正则 第十三节中, ...

  8. keras 添加L2正则 和 dropout层

    在某一层添加L2正则: from keras import regularizer model.add(layers.Dense(..., kernel_regularizer = regulariz ...

  9. 【深度学习】L1正则化和L2正则化

    在机器学习中,我们非常关心模型的预测能力,即模型在新数据上的表现,而不希望过拟合现象的的发生,我们通常使用正则化(regularization)技术来防止过拟合情况.正则化是机器学习中通过显式的控制模 ...

随机推荐

  1. VS------csc.exe已停止工作解决方法

    转载: http://blog.csdn.net/verylost/article/details/53667769 方法: 解决方法是把进程中所有的VBCSCompiler.exe进程结束掉,然后清 ...

  2. shell基础（八）-循环语句

    国庆过后:感觉有点慵懒些了:接着上篇:我们继续来学习循环语句. 一. for循环 与其他编程语言类似,Shell支持for循环. for循环一般格式为: for 变量 in 列表 do command ...

  3. 【RF库Collections测试】combine lists

    Arguments: [ *lists ]Combines the given `lists` together and returns the result. The given lists are ...

  4. docker run 详解

    docker run 用于把镜像启动为容器,语法如下: docker run [OPTIONS] IMAGE [COMMAND] [ARG...] 常见用法: [root@localhost ~]$ ...

  5. AndroidStudio遇到过的问题

    尊重原创 1.uses-sdk:minSdkVersion 1 cannot be smaller than version 4 declared in library [com.android.su ...

  6. CMS3.0——初次邂逅express

    前言: 刚接手cms3.0的工作,似乎对一切都那么的不熟悉,于是在开始新需求之前,先做一个简单的登录系统. 项目目录: 1.使用webstroms建expreess项目,非常方便简单,建好的项目目录就 ...

  7. MUI Hbuilder设置模拟器运行APP项目

    1 安装hbuilder和夜神模拟器 2 hbuilder  新建app项目 3 hbuilder:运行-> 设置web服务器->Hbuilder 第三方安卓模拟器端口:62001 4 运 ...

  8. java基础---->多个排序的拓展

    根据一些特定的规则,我们可以利用java的反射机制做到很有趣的封装. java的排序封装 一.定义一些comparator AmountComparatorAsc:amount升序 package c ...

  9. hihocoder [Offer收割]编程练习赛14 剑刃风暴

    题目4 : 剑刃风暴 时间限制:20000ms 单点时限:2000ms 内存限制:256MB 描述 主宰尤涅若拥有一招非常厉害的招式——剑刃风暴,“无论是战士还是法师,都害怕尤涅若的武士刀剑技”. 现 ...

  10. ntpdate自动对准时间的脚本

    author:headsen  chen date: 2018-10-09  19:50:15 #!/bin/bash yum -y install ntpdate /usr/sbin/ntpdate ...