Leetcode 188.买卖股票的最佳时机IV

买卖股票的最佳时机IV

给定一个数组，它的第 i 个元素是一支给定的股票在第 i 天的价格。

设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。

注意: 你不能同时参与多笔交易（你必须在再次购买前出售掉之前的股票）。

示例 1:

输入: [2,4,1], k = 2

输出: 2

解释: 在第 1 天 (股票价格 = 2) 的时候买入，在第 2 天 (股票价格 = 4) 的时候卖出，这笔交易所能获得利润 = 4-2 = 2 。

示例 2:

输入: [3,2,6,5,0,3], k = 2

输出: 7

解释: 在第 2 天 (股票价格 = 2) 的时候买入，在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。

随后，在第 5 天 (股票价格 = 0) 的时候买入，在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。

思路：定义两个二维变量，

last[j][i]，表示恰好在第j日完成第i次交易的最大收益。

total[j][i]，表示在第j日之前（含）完成i次交易的最大收益。

那么如何递归或者递推计算两个变量的值呢？我们先考虑total变量，第j日之前完成i次交易，可以分为两种情况，第一种情况是最后一日不作任何交易，第二种是最后一日完成第i次交易，则total[j][i] = max(total[j-1][i], last[j][i])，这个比较容易理解。如何计算last呢？我们可以按照倒数第二日的交易情况进行分类，分为倒数第二日完成第i次交易，以及倒数第二日不做任何交易。对于前者，我们可以观察如果倒数第二日的第i次交易推迟到第i日的获利情况；对于后者，我们可以观察倒数第二日买入，最后一日（第j日）卖出的情况，即：last[j][i] = max(0, last[j-1][i] + prices[j] - prices[j-1], total[j-1][i-1] + prices[j] - prices[j-1])。为什么会有0呢？因为我们的交易至少不能亏钱，如果一定要有交易的话，我们当天买入、当天卖出，至少是可以不亏的。但会不会有其他情况呢？例如最后一次交易有没有可能是倒数第三天买入，最后一天卖出？分析下面六种情况，可以知道公式是正确的。

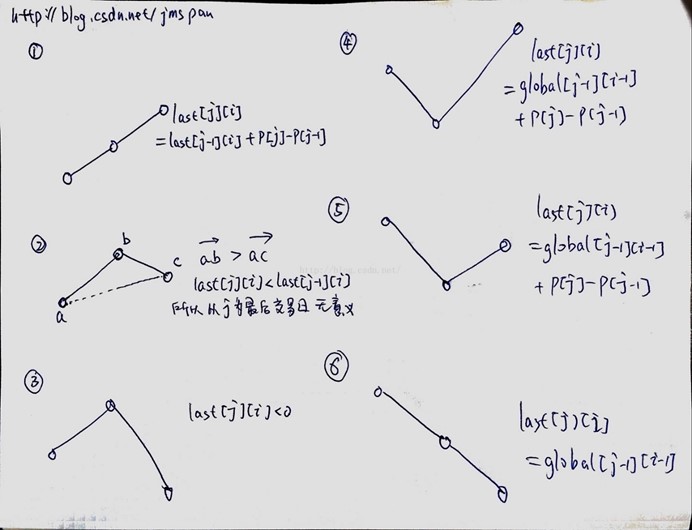
数据流演示：

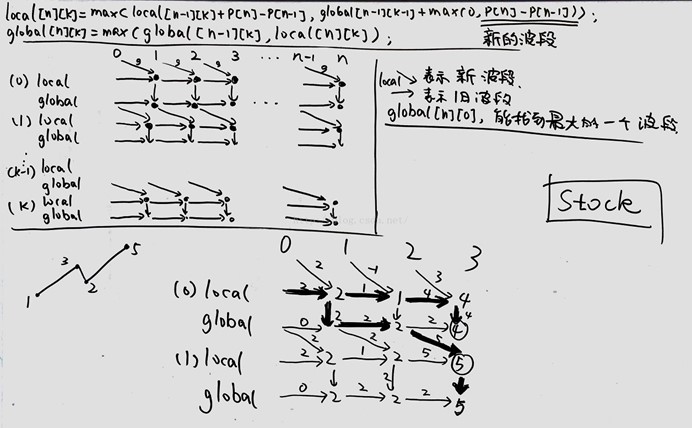
 public class Solution {
     private int max(int[] prices) {
         int max = 0;
         for(int i=1; i<prices.length; i++) {
             max += Math.max(0, prices[i] - prices[i-1]);
         }
         return max;
     }
     public int maxProfit(int k, int[] prices) {
         if (prices == null || prices.length < 2) return 0;
         int n = prices.length;
         if (k >= n/2) return max(prices);
         int[][] last = new int[n][k+1];
         int[][] total = new int[n][k+1];
         for(int t = 1; t <= k; t ++) {
             for(int d = 1; d < n; d ++) {
                 last[d][t] = Math.max(last[d-1][t] + prices[d] - prices[d-1], total[d-1][t-1] + Math.max(0, prices[d] - prices[d-1]));
                 total[d][t] = Math.max(total[d-1][t], last[d][t]);
             }
         }
         return total[n-1][k];
     }
 }