2-10 就业课(2.0)-oozie：2、介绍和安装1

oozie的安装及使用

1、  oozie的介绍

Oozie是运行在hadoop平台上的一种工作流调度引擎，它可以用来调度与管理hadoop任务，如，MapReduce、Pig等。那么，对于OozieWorkflow中的一个个的action（可以理解成一个个MapReduce任务）Oozie是根据什么来对action的执行时间与执行顺序进行管理调度的呢？答案就是我们在数据结构中常见的有向无环图(DAGDirect Acyclic Graph)的模式来进行管理调度的，我们可以利用HPDL语言（一种xml语言）来定义整个workflow，实现工作流的调度oozie的架构以及执行流程

2、oozie的架构

oozie的执行流程

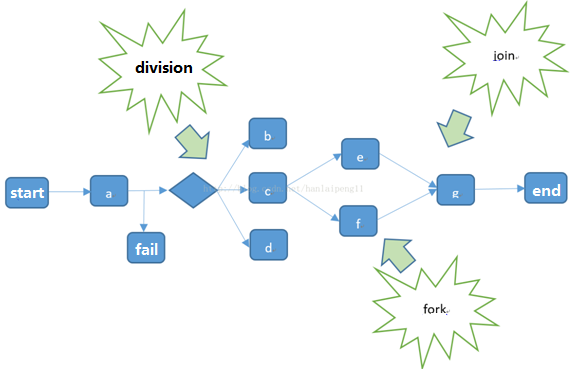
oozie的组件介绍

workFlow：工作流，定义我们的工作流的任务的执行，主要由一个个的action，在xml中进行配置即可

Coordinator ：协作器，说白了就是oozie当中的定时任务调度的模块

Bundle ：多个Coordinator 的抽象，可以通过bundle将多个Coordinator 进行组装集合起来，形成一个bundle。（用得很少）

3、oozie的安装

第一步：修改core-site.xml

修改core-site.xml添加我们hadoop集群的代理用户

cd /export/servers/hadoop-2.6.0-cdh5.14.0/etc/hadoop

vim  core-site.xml

<property>

<name>hadoop.proxyuser.root.hosts</name>

<value>*</value>

</property>

<property>

<name>hadoop.proxyuser.root.groups</name>

<value>*</value>

</property>

注意：hadoop的历史任务的服务必须启动，即19888端口可以查看，具体如何配置19888请查看hadoop课程的环境搭建

修改完成之后，记得重启hadoop的hdfs与yarn集群，还要记得启动jobhistory

重启hdfs与yarn集群

cd /export/servers/hadoop-2.6.0-cdh5.14.0

sbin/stop-dfs.sh

sbin/start-dfs.sh

sbin/stop-yarn.sh

sbin/start-yarn.sh

第二步：上传oozie的安装包并解压

将我们的oozie的安装包上传到/export/softwares

cd /export/softwares/

tar -zxvf oozie-4.1.0-cdh5.14.0.tar.gz -C ../servers/

第三步：解压hadooplibs到与oozie平行的目录

cd /export/servers/oozie-4.1.0-cdh5.14.0

tar -zxvf oozie-hadooplibs-4.1.0-cdh5.14.0.tar.gz -C ../

第四步：创建libext目录

在oozie的安装路径下创建libext目录

cd /export/servers/oozie-4.1.0-cdh5.14.0

mkdir -p libext

第五步：拷贝依赖包到libext

拷贝一些依赖包到libext目录下面去

拷贝所有的依赖包

cd /export/servers/oozie-4.1.0-cdh5.14.0

cp -ra hadooplibs/hadooplib-2.6.0-cdh5.14.0.oozie-4.1.0-cdh5.14.0/* libext/

拷贝mysql的驱动包

cp /export/servers/hive-1.1.0-cdh5.14.0/lib/mysql-connector-java-5.1.38.jar /export/servers/oozie-4.1.0-cdh5.14.0/libext/

第六步：添加ext-2.2.zip压缩包

拷贝ext-2.2.zip这个包到libext目录当中去

将我们准备好的软件ext-2.2.zip拷贝到我们的libext目录当中去