python汉诺塔问题的递归理解

一、问题背景

　　汉诺塔问题是源于印度一个古老传说。

　　源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

　　简单来说目的就是要我们把盘子按照规则从A移到C

二、思路

此处我用递归的思想理解汉诺塔问题。递归的思想容易理解，但是运用在代码上的算法并不是解决汉诺塔问题的最佳算法。

我们初定有n个盘子，把三个盘子从左到右分别标为A，B，C。

　　我们先思考，如果只有一个盘子放在A柱，要移动到C，应该A-->C

（1）首先根据大的盘子在下，小的盘子在上的目标，我们倒着想，想到要移动A最下面的盘子。要把A最下面的盘子移动到C，首先要把前n-1个盘子移动到B

（2）然后可以把第n盘从A移动到C了

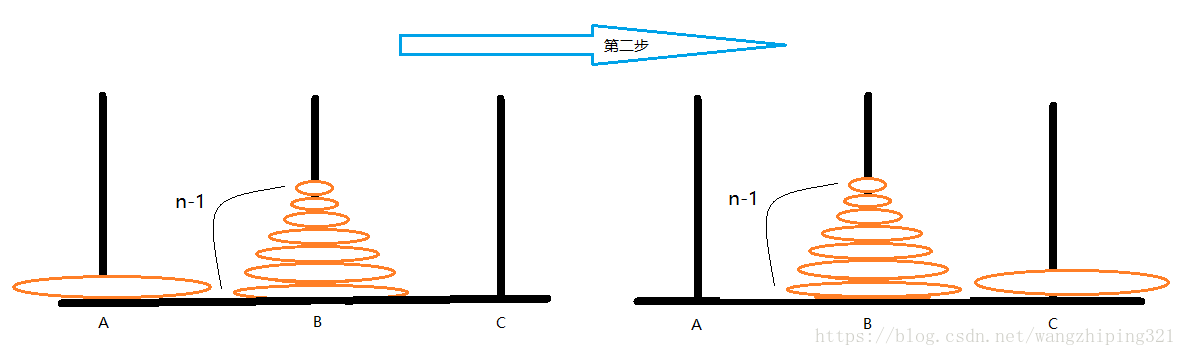
之后我们把B柱位置与A柱位置互换，我们可以发现忽略C中的盘子后，问题变为了n-1个盘子的汉诺塔问题

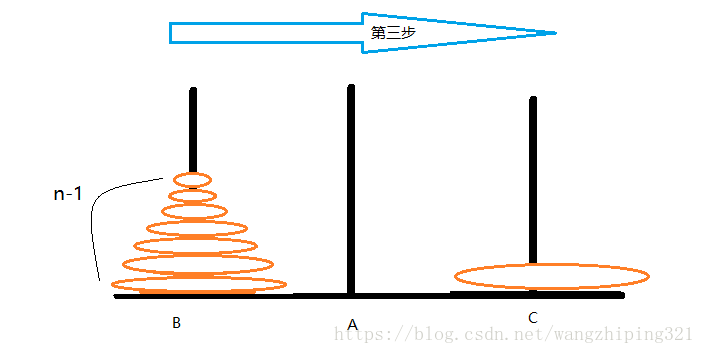
之后我们可以重复以上步骤，直至问题化为单一的盘子移动（从A到C）。

 三、python代码

此处我编写了一个hanoi函数和move函数去显示n个盘子的运动轨迹

n=eval(input())

def move(p,q):
print(p,'-->',q)
def hanoi(n,a,b,c):
if n==1:
move(a,c)
else:
hanoi(n-1,a,c,b)
move(a,c)
hanoi(n-1,b,a,c)
hanoi(n,'A','B','C')

四、效果

　　　　　　　　　　　　　5个盘子的移动轨迹显示