牛客网暑期ACM多校训练营（第十场）D Rikka with Prefix Sum （组合数学）

https://www.nowcoder.com/acm/contest/148/D

题意

一个A数组，初始全为0。现有三种操作，1：给区间[L，R]+w；2：把每个位置的元素变为其前缀和；3：求区间[L,R]的和

分析

参考：http://www.cnblogs.com/tetew/p/9504595.html

看到题的时候慌了神，因为1、2操作的可能次数实在太大了，认为是什么巧妙的数据结构。。。

实则是组合数学，脑子不够用啊。

首先我们讨论一下对某个位置的数进行+w的操作后，会对后面有什么影响。

纵列看作是2操作的次数，横排看作位置。45°斜着看，有点像杨辉三角！

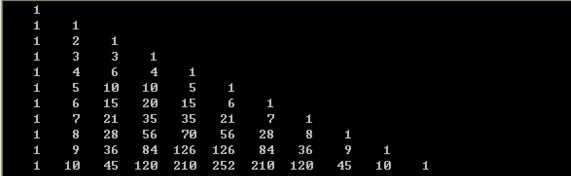
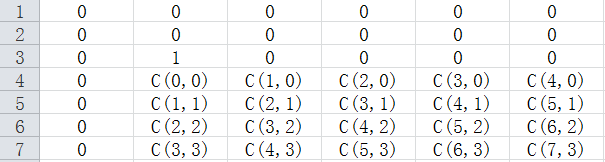
于是，如果在(i,j)+w，那么对于位于其右下方的点(x,y)来说，贡献为C(x-i+y-j-1,x-i-1)*w。

因为3操作不超过500次，我们记录1和2的操作，对于每次3操作，再O(n)查询。

求区间[L,R]的和时，可以直接solve(x+1,R)-solve(x+1,L-1),solve()是求前面所有的操作1和操作2的贡献，并且要加上这一次的求前缀和的贡献（所以是x+1）。

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <algorithm>
#include <cmath>
#include <ctime>
#include <vector>
#include <queue>
#include <map>
#include <stack>
#include <set>
#include <bitset>
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
#define ms(a, b) memset(a, b, sizeof(a))
#define pb push_back
#define mp make_pair
#define pii pair<int, int>
#define eps 0.0000000001
#define IOS ios::sync_with_stdio(0);cin.tie(0);
#define random(a, b) rand()*rand()%(b-a+1)+a
#define pi acos(-1)
const ll INF = 0x3f3f3f3f3f3f3f3fll;
const int inf = 0x3f3f3f3f;
const int maxn =  + ;
const int maxm =  + ;
const int mod = ;
ll fac[maxn],inv[maxn];
ll qpow(ll a,ll b){
    ll res=;
    while(b){
        if(b&) res=res*a%mod;
        b>>=;
        a=a*a%mod;
    }
    return res;
}
void init(){
   fac[]=;
   for(int i=;i<maxn;i++) fac[i]=fac[i-]*i%mod;
   inv[maxn-]=qpow(fac[maxn-],mod-);
   for(int i=maxn-;i>=;i--) inv[i]=inv[i+]*(i+)%mod;
}
ll C(int n,int m){
    if(m>n||m<) return ;
    return fac[n]*inv[m]%mod*inv[n-m]%mod;
}
struct ND{
    int x,pos,w;
}a[maxn];
int cnt;
ll cal(int x,int y){
    ll res=;
    for(int i=;i<=cnt;i++){
        if(a[i].x<=x&&a[i].pos<=y){
            res=(res+C(x-a[i].x+y-a[i].pos-,x-a[i].x-)*a[i].w%mod+mod)%mod;
        }
    }
    return res;
}
int main() {
#ifdef LOCAL
    freopen("in.txt", "r", stdin);
//    freopen("output.txt", "w", stdout);
#endif
    init();
    int T;
    int n,m,op,x,y;
    scanf("%d",&T);
    while(T--){
        scanf("%d%d",&n,&m);
        int now=;
        cnt=;
        while(m--){
            scanf("%d",&op);
            if(op==){
                scanf("%d%d%d",&x,&y,&op);
                a[++cnt].x=now-,a[cnt].pos=x,a[cnt].w=op;
                a[++cnt].x=now-,a[cnt].pos=y+,a[cnt].w=-op;
            }else if(op==){
                now++;
            }else{
                scanf("%d%d",&x,&y);
                ll ans=(cal(now+,y)-cal(now+,x-)+mod)%mod;
                printf("%lld\n",ans);
            }
        }
    }
    return ;
}