bzoj-1787-洛谷-4281（LCA板子题）

传送门（bzoj）

传送门（洛谷）

可以说这道也是一个板子题

由于题中是三个人需经过的路径最短

就会有一点点不太一样

那么

就两两求LCA

这样之后就会出现两种状况

一、所得到的三个LCA是相等的

　　那毫无疑问真正的LCA的值就是这个值

二、若不是第二种情况

　　那必然会出现

　　有且仅有一个LCA的值与令两个LCA的值不同

第二种情况正确性（不严格的）证明：

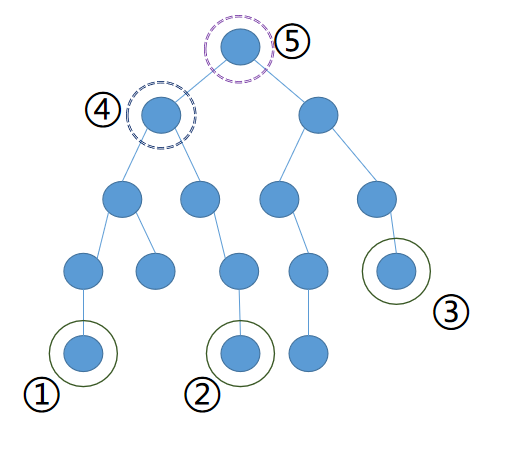
显然1和2的LCA是4

2和3的LCA是5

1和3的LCA也是5

既然2和3的LCA（5）的深度4大

那么也可把2和3的LCA看作是4和3的LCA

那么1和3的LCA也是5了

所以必定会有两个LCA是相同的

而且相同的那个一定是最高的

（因为 4和3的LCA是5 = 1和3的LCA是5 同时2 和3的LCA是5）

所以

找到了两个相同的

真正的LCA就是另一个

因为让3从5走到4

显然要比让1和2一起4走到5

同样都是要走4和5之间的相同的路径

只是方向不同而已

让1和2两个人一起走显然要比只要3走到长

所以真正的LCA是（与另外两个相同的LCA）不同的那个LCA，而不是相同的LCA了

然而当我信心满满写完的时候

我有sd了

需要减掉（即重复加到结果中的）被我简简单单的认为只是真正的LCA的深度*3

但是显然不是的啊

那这把是不是好了捏？

然而我输出的数不对啊

这可怎么回事？？

我方了

（在各种瞎调试之下）

我把每一个处理fa[ ][ ]数组的循环次数从20加到的25

奇迹般地好了

（这是为什么，明明样例数据很小的啊，怎么会影响到的呢？？）

跪求大佬们指点

这把终于过样例了

于是我开开心心的去提交了

结果re了

（又一脸懵）

于是我发现我sd的fa[ ][ ]数组忘再开大一点了

而且

由于是起初是无向图

所以

需要正反都要加边

但是我的数组只是一次加边的大小

既然就gg了

唉

什么时候可以不犯这种低级错误啊qwq...

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = ;
int hed[maxn * ],nxt[maxn * ],to[maxn * ],dep[maxn * ];
bool vis[maxn];
int fa[maxn][];
int n,m,cnt,rot;
inline int read()
{
    int sum = ,p = ;
    char ch = getchar();
    while(ch < '' || ch > '')
    {
        if(ch == '-')
            p = -;
        ch = getchar();
    }
    while(ch >= '' && ch <= '')
    {
        (sum *= )+= ch - '';
        ch = getchar();
    }
    return sum * p;
}
void add(int x,int y)
{
    nxt[++cnt] = hed[x];
    to[cnt] = y;
    hed[x] = cnt;
}
void dfs(int o,int k)
{
    dep[o] = dep[k] + ;
    for(int i = ;i<= ;i++)
        fa[o][i+] = fa[fa[o][i]][i];
    for(int i = hed[o];i;i = nxt[i])
    {
        if(to[i] == k)
            continue;
        fa[to[i]][] = o;
        dfs(to[i],o);
    }
}
int lca(int x,int y)
{
    if(dep[x] < dep[y])
        swap(x,y);
    for(int i = ;i >= ;i--)
    {
        if(dep[fa[x][i]] >= dep[y])
            x = fa[x][i];
        if(x == y)
            return x;
    }
    for(int i = ;i >= ;i--)
    {
        if(fa[x][i] != fa[y][i])
        {
            x = fa[x][i];
            y = fa[y][i];
        }
    }
    return fa[x][];
}
int main()
{
    n = read(),m = read();
    for(int i = ;i < n;i++)
    {
        int a = read(),b = read();
        add(a,b);
        add(b,a);
        vis[b] = ;
    }
    for(int i = ;i <= n;i++)
    {
        if(!vis[i])
        {
            rot = i;
            break;
        }
    }
    dep[rot] = ;
    dfs(rot,);
    for(int i = ;i <= m;i++)
    {
        int a = read(),b = read(),c = read();
        int o = lca(a,b);
        int p = lca(c,b);
        int q = lca(a,c);
        int u;
        if(o == p)
            u = q;
        else
        if(o == q)
            u = p;
        else
            u = o;
        printf("%d %d\n",u,dep[a] + dep[b] + dep[c]  - dep[o] - dep[p] - dep[q]);
    }
    return ;
}