[GKCTF2021]random

[GKCTF2021]random

本题出现了MT19937伪随机数生成算法。

目录

• [GKCTF2021]random
  • • • 题目
      • 分析
    • MT19937算法
      • 步骤
      • 代码实现
      • 解法1
      • 解法2
      • 总结

题目

task.py

import random
from hashlib import md5

def get_mask():
    file = open("random.txt","w")
    for i in range(104):	#各取104个
        file.write(str(random.getrandbits(32))+"\n")
        file.write(str(random.getrandbits(64))+"\n")
        file.write(str(random.getrandbits(96))+"\n")
    file.close()
get_mask()
flag = md5(str(random.getrandbits(32)).encode()).hexdigest()
print(flag)

random.txt

分析

感觉task.py没给啥，突破点在于这个random.getrandits()

去查一下得到：

random.getrandbits(k)

生成一个k比特长的随机整数

那也就意味着生成了32/64/96比特长的随机整数，32、64/96都是32的整数倍。

这会不会也是突破口呢？

看了wp，提到了一个算法：Mersenne Twister 梅森旋转算法

MT19937算法

产生随机数的速度快、周期长，可达到\(2^{19937-1}\)

可以产生32位整数序列，在$1\le k \le 623 $的维度之间都可以均等分布。

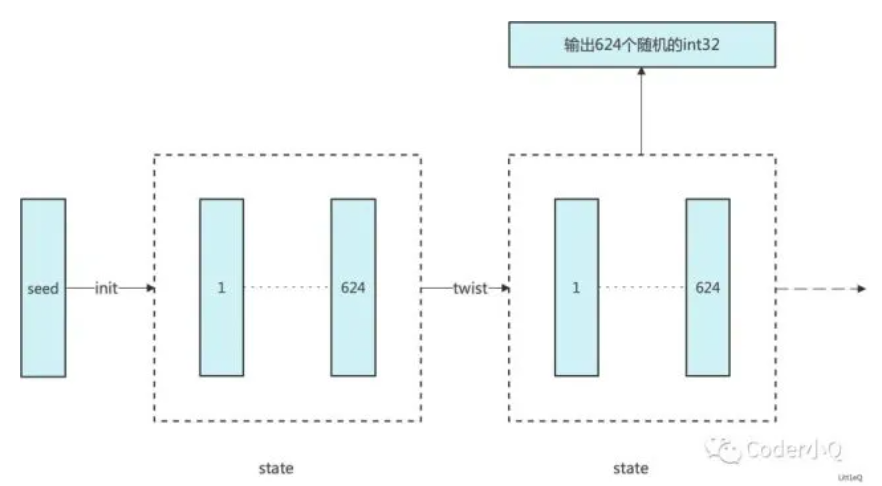
如上图所示，mt19937的随机数生成器结构首先需要一个uint32的种子，然后生成一个具有624个uint32数组的状态数组。生成状态数组之后，进行一次旋转，最终可以输出624个随机的uint32。然后重复执行旋转操作。

步骤

1.利用seed初始化624的状态

2.对状态进行旋转

3.根据状态提取伪随机数

代码实现

32位的MT19937的python代码如下：

def _int32(x):
    return int(0xFFFFFFFF & x)

class MT19937:
    # 根据seed初始化624的state
    def __init__(self, seed):
        self.mt = [0] * 624
        self.mt[0] = seed
        self.mti = 0
        for i in range(1, 624):
            self.mt[i] = _int32(1812433253 * (self.mt[i - 1] ^ self.mt[i - 1] >> 30) + i)

    # 提取伪随机数
    def extract_number(self):
        if self.mti == 0:
            self.twist()
        y = self.mt[self.mti]
        y = y ^ y >> 11
        y = y ^ y << 7 & 2636928640
        y = y ^ y << 15 & 4022730752
        y = y ^ y >> 18
        self.mti = (self.mti + 1) % 624
        return _int32(y)

    # 对状态进行旋转
    def twist(self):
        for i in range(0, 624):
            y = _int32((self.mt[i] & 0x80000000) + (self.mt[(i + 1) % 624] & 0x7fffffff))
            self.mt[i] = (y >> 1) ^ self.mt[(i + 397) % 624]

            if y % 2 != 0:
                self.mt[i] = self.mt[i] ^ 0x9908b0df

python中内置的Random类就是采用了MT19937算法，getrandbits(32)方法可以获得一个32位随机数

整个获取伪随机数的过程的重点就是这个self.mt[]也就是state块的状态。

在本题中，在random.txt中总共获取了312个随机数。其中有104个32位的，104个64位的，104个96位的。

解法1

因为本题随机数都是由32位整数序列产生，所以我们可以得知：

104个32位的需要产生104个随机数

104个64位的需要产生208个随机数

104个96位的需要产生312个随机数

所以总共需要产生624个随机数。

而这个数字刚刚好对应了624个state块的个数，理论上来讲，我们可以将624个state块的状态推出来，然后就可以推出下面产生的随机数，也就是flag了。

from random import Random

def invert_right(m,l,val=''):
    length = 32
    mx = 0xffffffff
    if val == '':
        val = mx
    i,res = 0,0
    while i*l<length:
        mask = (mx<<(length-l)&mx)>>i*l
        tmp = m & mask
        m = m^tmp>>l&val
        res += tmp
        i += 1
    return res

def invert_left(m,l,val):
    length = 32
    mx = 0xffffffff
    i,res = 0,0
    while i*l < length:
        mask = (mx>>(length-l)&mx)<<i*l
        tmp = m & mask
        m ^= tmp<<l&val
        res |= tmp
        i += 1
    return res

def invert_temper(m):
    m = invert_right(m,18)
    m = invert_left(m,15,4022730752)
    m = invert_left(m,7,2636928640)
    m = invert_right(m,11)
    return m

def clone_mt(record):
    state = [invert_temper(i) for i in record]
    gen = Random()
    gen.setstate((3,tuple(state+[0]),None))
    return gen

f = open("random.txt",'r').readlines()
prng = []
j=0
for i in f:
    i = i.strip('\n')
    print(int(i).bit_length())
    if(j%3==0):
        prng.append(int(i))
    elif(j%3==1):#将生成两次随机数的两个随机数分离出来
        prng.append(int(i)& (2 ** 32 - 1))
        prng.append(int(i)>> 32)
    else:#将生成三次随机数的三个随机数分离出来
        prng.append(int(i)& (2 ** 32 - 1))
        prng.append(int(i)& (2 ** 64 - 1) >> 32)
        prng.append(int(i)>>64)
    j+=1

g = clone_mt(prng[:624])
for i in range(624):
    g.getrandbits(32)#产生前624个随机数，让state状态到生成flag前

key = g.getrandbits(32)
print(key)
from hashlib import md5
flag = md5(str(key).encode()).hexdigest()
print(flag)
#14c71fec812b754b2061a35a4f6d8421

解法2

使用基于梅森算法的randcrack库。

randcrack一把梭：

from hashlib import md5
from randcrack import RandCrack

with open(r'random.txt', 'r') as f:
    l = f.readlines()
l = [int(i.strip()) for i in l]
t = []
for i in range(len(l)):
    if i % 3 == 0:
        t.append(l[i])
    elif i % 3 == 1:
        t.append(l[i] & (2 ** 32 - 1))
        t.append(l[i] >> 32)
    else:
        t.append(l[i] & (2 ** 32 - 1))
        t.append(l[i] & (2 ** 64 - 1) >> 32)
        t.append(l[i] >> 64)
rc = RandCrack()
for i in t:
    rc.submit(i)
flag = rc.predict_getrandbits(32)#在给出的随机数数量多时，predict_getrandbits()可以预测下一个随机数
print('GKCTF{'+md5(str(flag).encode()).hexdigest()+'}')

GKCTF{14c71fec812b754b2061a35a4f6d8421}

总结

有师傅的文章提到：近年来MT19937在各大CTF赛事中出现的频率越来越高。

那下次再做几道加深印象。

参考：https://www.anquanke.com/post/id/205861#h3-4

https://blog.csdn.net/m0_62506844/article/details/124278580?spm=1001.2101.3001.6650.5&utm_medium=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~default-5-124278580-blog-124983179.pc_relevant_multi_platform_whitelistv1&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2~default~BlogCommendFromBaidu~default-5-124278580-blog-124983179.pc_relevant_multi_platform_whitelistv1&utm_relevant_index=9