论文解读（MLGCL）《Multi-Level Graph Contrastive Learning》

论文信息

论文标题：Structural and Semantic Contrastive Learning for Self-supervised Node Representation Learning
论文作者： Kaize Ding 、Yancheng Wang 、Yingzhen Yang、Huan Liu
论文来源：2021, Neurocomputing
论文地址：download
论文代码：download

前言

　　本文贡献：

• 提出多层次图对比学习框架：联合节点级和图级对比学习；
• 图负样本定义；
• 引入 KNN 图提取语义信息；

1 介绍

　　本文开发了一个多层次的图对比学习（MLGCL）框架，用于通过对比图的拓扑视图和特征空间视图来学习图数据的鲁棒表示。如 Figure 2 所示，使用 KNN 算法对特征进行编码，从而在特征空间中生成 KNN 视图。KNN 视图不仅提供了互补视图，而且更适合GNN，将两者对比学习结合，可以显著提高 GNN 编码器的鲁棒性和适应性。

　　

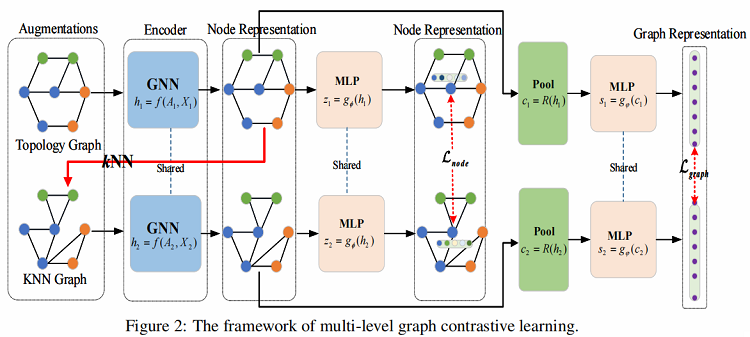
2 方法

　　框架流程

• 步骤一：从增强池 $\tau $ 中采样一对图增强函数 ${\tau }_{1}$ 和 ${\tau }_{2}$，并将其应用于输入图，生成两个视图的增广图；　　
• 步骤二：使用一对共享的 GNN 编码器来提取节点表示，并进一步利用池化层来提取图表示；　　
• 步骤三：利用一个共享参数的 MLP 层来将两个视图中的节点表示投影到计算节点级对比损失的空间中。类似地，还将来自两个视图的图表示投影到计算图级对比损失的空间中；　　
• 步骤四：通过优化所提出的多级损失函数来学习编码器的参数；

　　MLGCL主要由以下组成部分组成：

• 图数据增强：对输入图施加扰动，生成同一图的两个相关图。在本工作中，我们从空间视图中提取增强图结构来进行对比学习；
• GNN编码器：使用基于GNN的编码器 $f(\cdot)$ 来学习两个增广图的节点表示 $z_{1}$、$z_{2}$；
• MLP：投影头 MLP 层 $g(\cdot)$ 将表示法映射到计算对比损失的空间；　　
• 图池化：使用图池化层 $ R(\cdot)$ 来学习图的表示；
• 损失函数：提出了多级损失函数，同时保持“局部”和“全局”信息；

2.1 图数据增强

　　给定 $G(A、X)$ 的图结构，先利用 GNN 编码器提取拓扑图的编码特征 $Z$，然后利用 $\text{KNN}$ 对 $Z$ 的近邻构造 $\text{KNN}$ 图（$G_{f}\left(A_{f}, X\right)$），其中 $A_{f}$ 为 $\text{KNN}$ 图的邻接矩阵。

　　构建 $\text{KNN}$ 图可以描述为两个步骤:

• 首先，基于 $ N$ 个编码特征 $ Z $ 计算相似度矩阵 $S$；
• 其次，为每个节点选择前 $k$ 个相似的节点对来设置边，最后得到 $\text{KNN}$ 图的邻接矩阵 $A_{f} $ ；

　　事实上，得到相似度矩阵 $S$ 有许多方案，如基于距离的相似度计算方法（即欧氏距离，马氏距离)，基于余弦的相似度计算（即余弦相似 性，皮尔逊相关性）和基于核的相似性计算（即高斯核，拉普拉斯核）。这里列出三种流行的方法，其中 $x_{i} $ 和 $x_{j} $ 是节点 $i$ 和 $j$ 的 特征向量：

• 马氏距离

　　　　$S_{i j}=\sqrt{\left(x_{i}-x_{j}\right)^{T} M\left(x_{i}-x_{j}\right)}$

　　其中 $M$ 是一个正半定矩阵，它起着逆协方差矩阵的作用。 (如果 $M$ 是单位矩阵，则为欧氏距离)
　　正半定矩阵：设 $A$ 是 $n$ 阶方阵，如果对任何非零向量 $X$，都有 $X ' A X \geq 0$ ，其中 $X ' $ 表示 $X$ 的转置，就称 $A$ 为半正定矩阵。

• 余弦相似性

　　使用两个向量之间夹角的余弦值来度量相似性：

　　　　${\large S_{i j}=\frac{x_{i} \cdot x_{j}}{\left|x_{i}\right|\left|x_{j}\right|}} $

• 高斯核

　　　　${\large S_{i j}=e^{-\frac{\left\|x_{i}-x_{j}\right\|^{2}}{2 \sigma^{2}}}} $

　　其中， $\sigma$ 是高斯核的核宽度。

　　本文选择余弦相似性来得到相似性矩阵 $S$ 。

2.2 编码器

　　给定拓扑图 $G(A, X)$ 和 $\text{KNN}$图 $G_{f}\left(A_{f}, X\right)$ ，使用双层 GCN 作为编码器模型获得它们的潜在节点表示矩阵。编码器 $f(\cdot) $ 表示如下:

　　　　$Z^{l+1}=f(A, X)=\sigma\left(\widetilde{A} Z^{l} W^{l}\right)$

　　其中：$\widetilde{A}=\widehat{D}^{-1 / 2} \widehat{A} \widehat{D}{ }^{-1 / 2}$ 是对称归一化的邻接矩阵。

　　对于每个视图的节点表示 $Z_{a} $， $Z_{b} $ ，使用一个图池化层 $ P(\cdot): \mathbb{R}^{N \times d} \rightarrow \mathbb{R}^{d}$ (即读出函数)，得到它们的图表示:

　　　　$c=P(H)=\sigma\left(\frac{1}{N} \sum_{i=1}^{N} h_{i}\right)$

　　此外，为了对两个视图进行相应的节点表示和图表示对比，使用 MLP 层  $g_{\phi}(\cdot) 和 g_{\varphi}(\cdot): \mathbb{R}^{N \times d} \rightarrow \mathbb{R}^{N \times d}$   将节点和图表示分别投影到计算对比损失的空间中。

2.3 多级损失函数

　　多级损失函数，由两部分组成：两个视图之间低级节点表示的对比，以及两个视图之间高级图表示的对比。

　　低级节点表示的对比：给定正对 $(z_i、z_j)$，将节点级对比损失函数定义为

　　　　${\large \mathcal{L}_{\text {node }}\left(z_{i}^{a}, z_{i}^{b}\right)=\log \frac{\exp \left(\left(z_{i}^{a}\right)^{T} z_{i}^{b} / \tau\right)}{\sum_{j=1, j \neq i}^{K} \exp \left(\left(z_{i}^{a}\right)^{T} z_{i}^{b} / \tau\right)+\exp \left(\left(z_{i}^{a}\right)^{T} z_{j}^{a} / \tau\right)+\exp \left(\left(z_{i}^{a}\right)^{T} z_{j}^{b} / \tau\right)}} $

　　由于两个视图是对称的，所以另一个视图的损失被定义为 $L_{n o d e}\left(z_{i}^{b}, z_{i}^{a}\right)$ 。因此，通过优化以下内容，实现最大化两个视图之间的节点的一致性:

　　　　$\mathcal{L}_{n o d e}=\mathcal{L}_{n o d e}\left(z_{i}^{a}, z_{i}^{b}\right)+\mathcal{L}_{n o d e}\left(z_{i}^{b}, z_{i}^{a}\right)$

　　高级图表示的对比：给定正例  $\left(s^{a}, s^{b}\right)$  和负例  $\left(s^{a}, \tilde{s}^{a}\right)$ ，$\left(s^{a}, \tilde{s}^{b}\right)$  ，两个视图之间的图表示对比被定义为：

　　　　${\large \mathcal{L}_{\text {graph }}\left(s^{a}, s^{b}\right)=\log \frac{\exp \left(\left(s^{a}\right)^{T} s^{b} / \tau\right)}{\exp \left(\left(s^{a}\right)^{T} s^{b} / \tau\right)+\exp \left(\left(s^{a}\right)^{T} \tilde{s}^{a} / \tau\right)+\exp \left(\left(s^{a}\right)^{T} \tilde{s}^{b} / \tau\right)}} $

　　本文为生成图的负样本，随机 shuffle 特征以推导出负邻接矩阵 $\widetilde{A}$ 和 $\widetilde{A}_{f}$ ，然后得到负样本 $\left(s^{a}, \tilde{s}^{a}\right) ，\left(s^{a}, \tilde{s}^{b}\right) $ 。由于对称性，另一个视图的损失被定义为 $L_{g r a p h}\left(s^{b}, s^{a}\right) $ 。因此，整体图表示对比为:

　　　　$\mathcal{L}_{g r a p h}=\mathcal{L}_{g r a p h}\left(s^{a}, s^{b}\right)+\mathcal{L}_{g r a p h}\left(s^{b}, s^{a}\right)$

　　最后，通过将节点级对比损失与图级对比损失相结合，模型的多级损失为：

　　　　$\mathcal{L}=\mathcal{L}_{\text {node }}+\lambda \mathcal{L}_{\text {graph }}$

3 实验

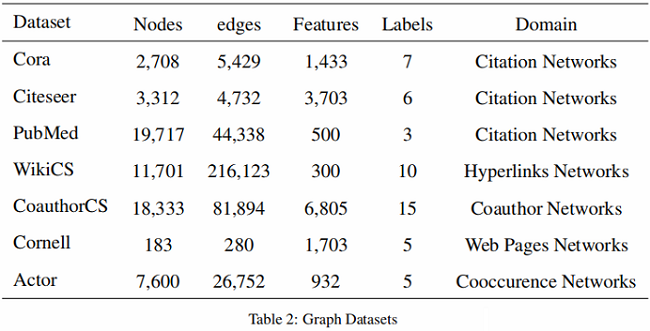
3.1 数据集

　　

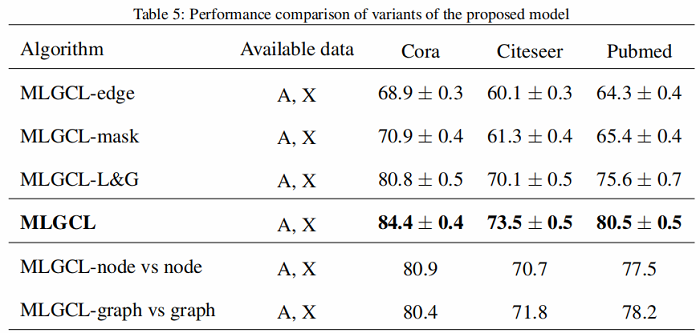
3.2 结果

　　

　　

　　

4 结论

　　学到：

• 提出多层次图对比学习框架：联合节点级和图级对比学习；
• 图负样本定义；
• 引入 $\text{KNN}$ 图提取语义信息；　　

5 相关论文

2016-AAAI——Deep neural networks for learning graph representations
2021-WWW——Graph structure estimation neural networks
2017-NIPS——Inductive representation learning on large graphs