第二十三篇 玩转数据结构——栈（Stack）
- 栈也是一种线性结构；
- 相比数组，栈所对应的操作是数组的子集；
- 栈只能从一端添加元素，也只能从这一端取出元素，这一端通常称之为"栈顶"；
- 向栈中添加元素的过程，称之为"入栈"，从栈中取出元素的过程称之为"出栈"；
- 栈的形象化描述如下图：
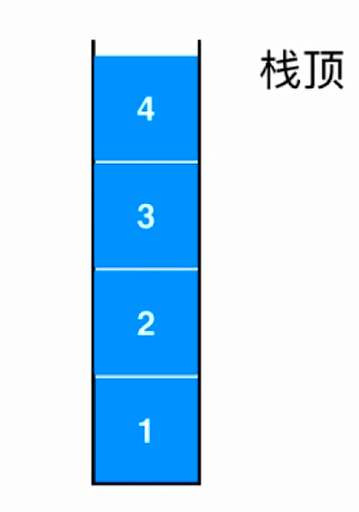
- "入栈"的顺序若为1-2-3-4，那么出栈的顺序只能为4-3-2-1，即，栈是一种"后进先出"（Last In First Out）的数据结构；
- 从用户的角度，只能看到栈顶元素，其它元素对用户是不可见的；
- 在计算机世界里，"栈"有着不可思意的作用；
- 应用程序中的"撤销"(Undo)操作的底层原理就是通过"栈"来实现的；
- 程序调用的系统栈，通过下图简单示例：
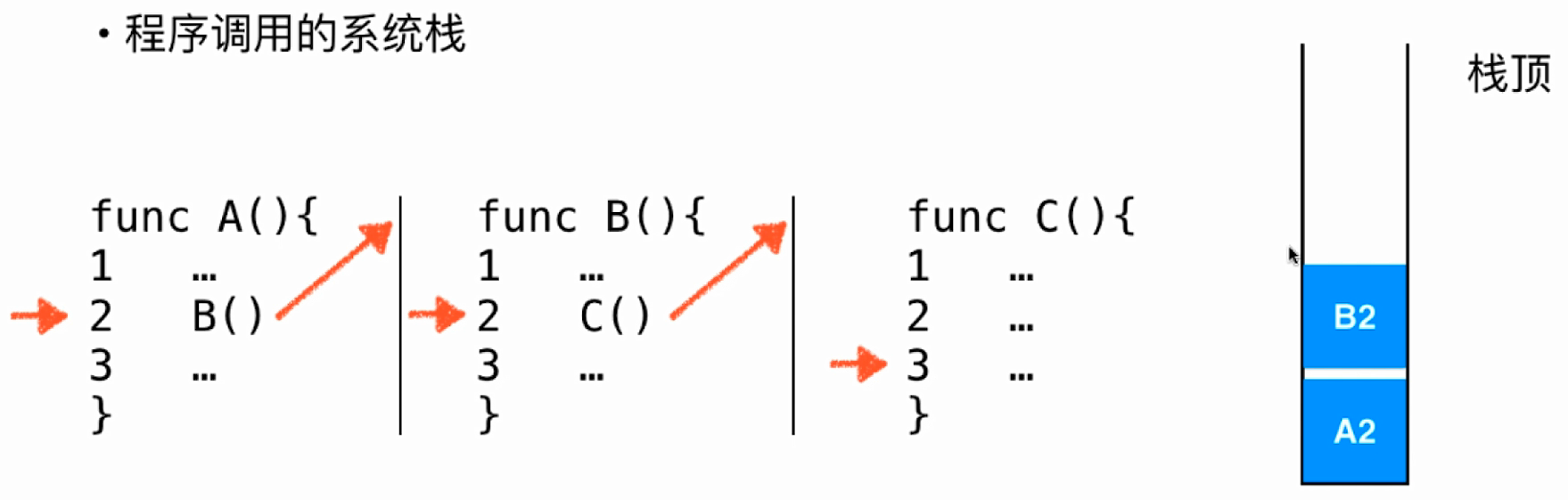
- 任务目标如下：
Stack<E>
·void push(E) //入栈
·E pop() // 出栈
·E peek() // 查看栈顶元素
·int getSize() // 查看栈中共有多少元素
·boolean isEmpty() // 查看栈是否为空
- 需要提一下，从用户的角度来看，只要实现上述操作就好，具体底层实现，用户并不关心，实际上，底层确实有多种实现方式。
- 我们准备在之前实现的动态数组基础上，来实现"栈"这种数据结构。
- 先定义一个接口Interface，如下：
public interface Stack<E> { // 支持泛型
int getSize(); boolean isEmpty(); void push(E e); E pop(); E peek();
}- 然后实现一个ArrayStack类，如下：
public class ArrayStack<E> implements Stack<E> {
Array<E> array; //构造函数
public ArrayStack(int capacity) {
array = new Array<>(capacity);
} //无参数构造函数
public ArrayStack() {
array = new Array<>();
} //实现getSize方法
@Override
public int getSize() {
return array.getSize();
} //实现isEmpty方法
@Override
public boolean isEmpty() {
return array.isEmpty();
} //实现getCapacity方法
public int getCapacity() {
return array.getCapacity();
} //实现push方法
@Override
public void push(E e) {
array.addLast(e);
} //实现pop方法
@Override
public E pop() {
return array.removeLast();
} //实现peek方法
public E peek() {
return array.getLast();
} //方便打印测试
@Override
public String toString() {
StringBuilder res = new StringBuilder();
res.append("Stack: ");
res.append('[');
for (int i = 0; i < array.getSize(); i++) {
res.append(array.get(i));
if (i != array.getSize() - 1) {
res.append(", ");
}
}
res.append("] top");
return res.toString();
}
}- Array类的业务逻辑如下：
public class Array<E> { private E[] data; //设置为private，不希望用户从外部直接获取这些信息，防止用户篡改数据
private int size; //构造函数，传入数组的容量capacity构造Array
public Array(int capacity) {
data = (E[]) new Object[capacity];
size = 0;
} //无参数构造函数，默认数组容量capacity=10
public Array() {
this(10); //这里的capacity是IDE自动添加的提示信息，实际不存在
} //获取数组中的元素个数
public int getSize() {
return size;
} //获取数组的容量
public int getCapacity() {
return data.length;
} //判断数组是否为空
public boolean isEmpty() {
return size == 0;
} //向数组末尾添加一个新元素e
public void addLast(E e) {
add(size, e);
} //向数组开头添加一个新元素e
public void addFirst(E e) {
add(0, e);
} //在index位置插入一个新元素e
public void add(int index, E e) { if (index < 0 || index > size) {
throw new IllegalArgumentException("Add failed. Require index >= 0 and index <= size");
}
if (size == data.length) {
resize(2 * size); //扩大为原容量的2倍
}
for (int i = size - 1; i >= index; i--) {
data[i + 1] = data[i];
}
data[index] = e;
size++;
} //获取index位置的元素
public E get(int index) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Get failed. Index is illegal.");
}
return data[index];
} //获取最后一个元素
public E getLast() {
return get(size - 1);
} //获取开头的元素
public E getFirst() {
return get(0);
} //修改index位置的元素为e
public void set(int index, E e) {
if (index < 0 || index >= size) {
throw new IllegalArgumentException("Set failed. Index is illegal.");
}
data[index] = e;
} //查找数组中是否存在元素e
public boolean contains(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return true;
}
}
return false;
} //查看数组中元素e的索引，若找不到元素e，返回-1
public int find(E e) {
for (int i = 0; i < size; i++) {
if (data[i].equals(e)) {
return i;
}
}
return -1;
} //删除掉index位置的元素，并且返回删除的元素
public E remove(int index) { if (index < 0 || index >= size) {
throw new IllegalArgumentException("Remove failed. Index is illegal.");
} E ret = data[index]; for (int i = index + 1; i < size; i++) {
data[i - 1] = data[i];
}
size--; //data[size]会指向一个类对象，这部分空间不会被释放loitering objects
data[size] = null; if (size == data.length / 4 && data.length / 2 != 0) {
resize(data.length / 2); //被利用的空间等于总空间的一半时，将数组容量减少一半
}
return ret;
} //删除掉数组开头的元素，并返回删除的元素
public E removeFirst() {
return remove(0);
} //删除掉数组末尾的元素，并返回删除的元素
public E removeLast() {
return remove(size - 1);
} //如果数组中有元素e，那么将其删除，否则什么也不做
public void removeElement(E e) {
int index = find(e);
if (index != -1) {
remove(index);
}
} @Override
public String toString() { //覆盖父类的toString方法 StringBuilder res = new StringBuilder();
res.append(String.format("Array: size=%d, capacity=%d\n", size, data.length));
res.append('[');
for (int i = 0; i < size; i++) {
res.append(data[i]);
if (i != size - 1) {
res.append(", ");
}
}
res.append(']');
return res.toString();
} private void resize(int newCapacity) {
E[] newData = (E[]) new Object[newCapacity];
for (int i = 0; i < size; i++) {
newData[i] = data[i];
}
data = newData;
}
}
4.. 对我们实现的栈进行测试：
public class Main { public static void main(String[] args) { ArrayStack<Integer> stack = new ArrayStack<>(); //测试入栈push
for (int i = 0; i < 5; i++) {
stack.push(i);
System.out.println(stack);
} //测试出栈
stack.pop();
System.out.println(stack);
}
}- 输出结果如下：
Stack: [0] top
Stack: [0, 1] top
Stack: [0, 1, 2] top
Stack: [0, 1, 2, 3] top
Stack: [0, 1, 2, 3, 4] top
Stack: [0, 1, 2, 3] top
5.. 栈的时间复杂度分析
Stack<E>
·void push(E) O(1) 均摊
·E pop() O(1) 均摊
·E peek() O(1)
·int getSize() O(1)
·boolean isEmpty() O(1)
- 业务逻辑如下：
import java.util.Stack; class Solution {
public boolean isValid(String s) {
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char c = s.charAt(i);
if (c == '(' || c == '[' || c == '{') {
stack.push(c);
} else {
if (stack.isEmpty()) {
return false;
}
char topChar = stack.pop();
if (topChar == '(' && c != ')') {
return false;
}
if (topChar == '[' && c != ']') {
return false;
}
if (topChar == '{' && c != '}') {
return false;
}
}
}
return stack.isEmpty(); //这里很巧妙
} //测试
public static void main(String[] args){
System.out.println((new Solution()).isValid("()"));
System.out.println((new Solution()).isValid("()[]}{"));
System.out.println((new Solution()).isValid("({[]})"));
System.out.println((new Solution()).isValid("({)}[]")); }
}
第二十三篇 玩转数据结构——栈（Stack）的更多相关文章
- 第二十七篇 玩转数据结构——集合（Set）与映射（Map）
1.. 集合的应用 集合可以用来去重 集合可以用于进行客户的统计 集合可以用于文本词汇量的统计 2.. 集合的实现 定义集合的接口 Set<E> ·void add(E) ...
- 第三十三篇 玩转数据结构——红黑树（Read Black Tree）
1.. 图解2-3树维持绝对平衡的原理: 2.. 红黑树与2-3树是等价的 3.. 红黑树的特点 简要概括如下: 所有节点非黑即红:根节点为黑:NULL节点为黑:红节点孩子为黑:黑平衡 4.. 实现红 ...
- Python开发【第二十三篇】：持续更新中...
Python开发[第二十三篇]:持续更新中...
- 第二十五篇 玩转数据结构——链表（Linked List）
1.. 链表的重要性 我们之前实现的动态数组.栈.队列,底层都是依托静态数组,靠resize来解决固定容量的问题,而"链表"则是一种真正的动态数据结构,不需要处理固定容 ...
- 第二十六篇 玩转数据结构——二分搜索树（Binary Search Tree）
1.. 二叉树 跟链表一样,二叉树也是一种动态数据结构,即,不需要在创建时指定大小. 跟链表不同的是,二叉树中的每个节点,除了要存放元素e,它还有两个指向其它节点的引用,分别用Node l ...
- 第二十八篇 玩转数据结构——堆（Heap）和有优先队列(Priority Queue)
1.. 优先队列(Priority Queue) 优先队列与普通队列的区别:普通队列遵循先进先出的原则:优先队列的出队顺序与入队顺序无关,与优先级相关. 优先队列可以使用队列的接口,只是在 ...
- 第二十四篇 玩转数据结构——队列（Queue）
1.. 队列基础 队列也是一种线性结构: 相比数组,队列所对应的操作数是队列的子集: 队列只允许从一端(队尾)添加元素,从另一端(队首)取出元素: 队列的形象化描述如下图: 队列是一种先进 ...
- 第二十九篇 玩转数据结构——线段树（Segment Tree）
1.. 线段树引入 线段树也称为区间树 为什么要使用线段树:对于某些问题,我们只关心区间(线段) 经典的线段树问题:区间染色,有一面长度为n的墙,每次选择一段墙进行染色(染色允许覆盖),问 ...
- C# 数据结构 栈 Stack
栈和队列是非常重要的两种数据结构,栈和队列也是线性结构,线性表.栈和队列这三种数据结构的数据元素和元素的逻辑关系也相同 差别在于:线性表的操作不受限制,栈和队列操作受限制(遵循一定的原则),因此栈和队 ...
随机推荐
- XSS进阶学习-转载
在这篇帖子里面真的可以学到很多xss的知识,特别有过xss基础的看完这个贴子绝对有帮助: 就像里面的师傅所说,看了一篇精髓文章之后,自己xss的功力突飞猛进了. 所提到的帖子入口:https://mp ...
- 请求 - axios
实际应用示例 前端不需要做统一的接口防重 前端无法通过判断接口是否返回来释放按钮(因为可以手动刷新页面,将导致刷新前请求丢失) 后端对接口做了防重 通过增加时间戳避免IE9的get请求缓存问题 axi ...
- Myeclipse连接Mysql数据库时报错：Error while performing database login with the pro driver:unable
driver template: Mysql connector/j(下拉框进行选择) driver name: 任意填,最好是数据库名称,方便查找 connection URL: jdbc:mysq ...
- SequoiaDB巨杉数据库入门：快速搭建流媒体服务器
使用SequoiaDB的分布式文件系统搭建流媒体服务器 介绍 如今使用移动互联网的年轻人开始越来越多使用短视频展示自我,而流媒体则是支撑在线视频播放的核心技术.当我们开始构建流媒体站点时,往往面临最大 ...
- JavaScript的流程控制
JavaScript的流程控制 1.if...else if...else... 2.while 3.for 4.forEach 5.for...in... 完整代码如下: <!DOCTYPE ...
- bootstrap4的改进
- 移动 APP 端与服务器端用户身份认证的安全方案
最近要做一个项目是java开发后端服务,然后移动APP调用.由于之前没有接触过这块,所以在网上搜索相关的方案.然后搜到下面的一些方案做一些参考. 原文:移动 APP 端与服务器端用户身份认证的安全方案 ...
- C++ 跨dll传递string类型参数执行出错问题
今天遇到一个问题,在一个dll工程中定义了一个返回值为string,参数为string的函数,然后在一个测试工程中调用,Release模式下一切正常Debug模式下整个函数的执行到return之前都毫 ...
- 第五篇，理解JS模块化编程思想
模块化编程 ·模块化编程是一种处理复杂系统分解成更好的可管理模块的方式,它可以把系统代码划分为职责单一高度解耦切可替代的模块. ·系统中某一部分的变化将如何影响其他部分就会变得显而易见,系统的可维护性 ...
- vue-cli脚手架创建vue项目
CLI 使用vue-cli可以快速搭建Vue开发环境以及对应的webpack配置 cnpm install -g @vue/cli // 如果需要使用旧版本的vue init功能(脚手架2),你可以全 ...