关于Floyd求解最小环的问题

最近学习了floyd的奇妙用处，求解最小环，自己的领悟写在了纸上。

对于一个最小环，显然至少要包含三个点(此处不把两个点的回路称之为环)

从大体上考虑的话，一定有一个点与左右两侧的点是直接连接的(即不经其他点的松弛),我们不妨设这个点为k

对于floyd,也是也k的遍历作为松弛条件,所以考虑使用floyd求解最小环，显然k是逐渐增大的，也就是说除去k点的那个环剩下的那条最短路中一定不能有k，

否则会出现不是环的路径被错误的判定为环   ，如下图:

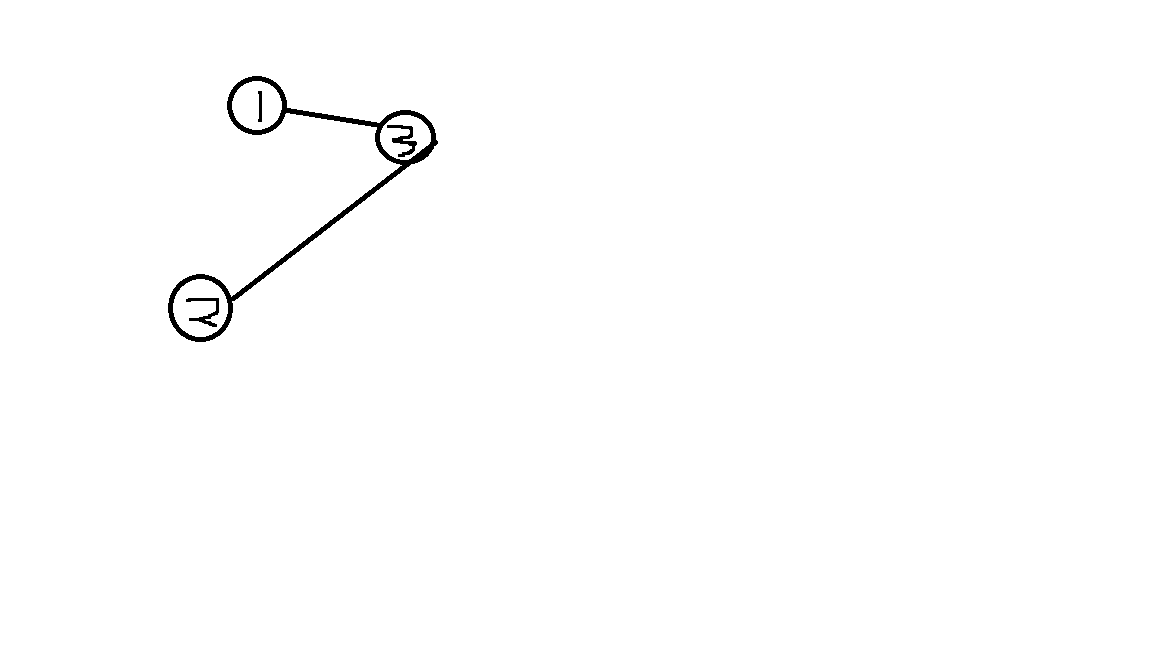
假设3已经成功的将1，2松弛，再次利用3来计算最小环时显然此时计算出的s=dis[1][3]+e[1][3]+e[3][2];

但显然这不是一个环啊，所以这就解释了这个算法里第一个for里面i,j都只是循环到k-1的原因.

#include<bits/stdc++.h>  //以hdu1599为例，切记别爆  inf*3即可
using namespace std;
#define inf 99999999
int e[105][105];
int dis[105][105];
int main()
{
int n,m,i,j,k;
while(cin>>n>>m){int a,b,c;
for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
if(i==j) e[i][j]=dis[i][j]=0;
else e[i][j]=dis[i][j]=inf;
for(i=1;i<=m;++i) {
cin>>a>>b>>c;
if(c>e[a][b]) continue;
e[a][b]=e[b][a]=dis[a][b]=dis[b][a]=c;
} int ans=inf;
for(k=1;k<=n;++k)
{
for(i=1;i<k;++i)
for(j=i+1;j<k;++j)
ans=min(ans,dis[i][j]+e[i][k]+e[k][j]);
for(i=1;i<=n;++i)
for(j=1;j<=n;++j)
dis[i][j]=min(dis[i][j],dis[i][k]+dis[k][j]);
}
if(ans==inf) puts("It's impossible.");
else cout<<ans<<endl;
}
return 0;
}

上面说的是对于无向图，那么有向图呢，也是如此吗？显然不成立，

对于上面代码红色部分，这个j之所以从i+1开始就可以了是因为无向图的对称性质，而有向图并不具有这个性质，所以需要改动.

但是要是仔细想想的话，有向图的最小环其实只要直接跑一遍floyd，然后遍历一遍dis[i][i]即可，因为图是无向的所以不必担心出现重边啊

//vjos1423为例

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
int e[210][210];
int w[210];
int main()
{
	int n,m,i,j,k;
	cin>>n>>m;
	memset(e,inf,sizeof(e));
	for(i=1;i<=n;++i) cin>>w[i];
	for(i=1;i<=m;++i){
		int a,b,c;
		cin>>a>>b>>c;
		e[a][b]=min(e[a][b],c+w[a]);
	}int ans=inf;
	 for(k=1;k<=n;++k)
	      for(i=1;i<=n;++i)
	         for(j=1;j<=n;++j)
	         	e[i][j]=min(e[i][j],e[i][k]+e[k][j]);
  // e[i][j]=min(e[i][j],e[i][k]+e[k][j]);

  // for(i=2;i<=n;++i) ans=min(ans,e[1][i]+e[i][1]);
   printf("%d\n",e[1][1]==inf?-1:e[1][1]);
	return 0;
}