Educational Codeforces Round 40 C. Matrix Walk( 思维)

Educational Codeforces Round 40 (Rated for Div. 2)

C. Matrix Walk

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

There is a matrix A of size x × y filled with integers. For every 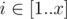, 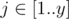A**i, j = y(i - 1) + j. Obviously, every integer from [1..xy] occurs exactly once in this matrix.

You have traversed some path in this matrix. Your path can be described as a sequence of visited cells a1, a2, ..., a**n denoting that you started in the cell containing the number a1, then moved to the cell with the number a2, and so on.

From the cell located in i-th line and j-th column (we denote this cell as (i, j)) you can move into one of the following cells:

1. (i + 1, j) — only if i < x;
2. (i, j + 1) — only if j < y;
3. (i - 1, j) — only if i > 1;
4. (i, j - 1) — only if j > 1.

Notice that making a move requires you to go to an adjacent cell. It is not allowed to stay in the same cell. You don't know x and y exactly, but you have to find any possible values for these numbers such that you could start in the cell containing the integer a1, then move to the cell containing a2 (in one step), then move to the cell containing a3 (also in one step) and so on. Can you choose x and y so that they don't contradict with your sequence of moves?

Input

The first line contains one integer number n (1 ≤ n ≤ 200000) — the number of cells you visited on your path (if some cell is visited twice, then it's listed twice).

The second line contains n integers a1, a2, ..., a**n (1 ≤ a**i ≤ 109) — the integers in the cells on your path.

Output

If all possible values of x and y such that 1 ≤ x, y ≤ 109 contradict with the information about your path, print NO.

Otherwise, print YES in the first line, and in the second line print the values x and y such that your path was possible with such number of lines and columns in the matrix. Remember that they must be positive integers not exceeding 109.

Examples

input

Copy

81 2 3 6 9 8 5 2

output

Copy

YES3 3

input

Copy

61 2 1 2 5 3

output

Copy

NO

input

Copy

21 10

output

Copy

YES4 9

Note

The matrix and the path on it in the first test looks like this:

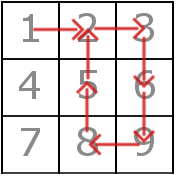
Also there exist multiple correct answers for both the first and the third examples.

题意：

有一个很大的方格，x行，y列，以及a(i,j)=(i-1)*y+j

现在给你n个数的数组，代表在方格中只走相邻节点的路径经过的节点数值，，让你是否能确定一个x和y，如果有，则输出对应的x和y，否则输出no。

思路：

如果是一个合法的路径序列，那么相邻的节点的数值之差的绝对值只可能是1和y，

如果差的绝对值size有多个值（即大于2），或者有2个值但没有1，那么一定是不存在的。

接下来就是size<=2的情况了，

假设y=size 中较大的那一个（如果相等，即都为1，那么直接特判输出答案即可，），

去再从1到n扫check下如果y是该值，是否满足该序列，

注意一下情况：

当前在左边界num，向num-1走

当前在右边界num，向num+1走

都是不合法的（已经排除了y=1的情况）

然后输出即可。

get：一般给你一些信息，让你确定一些值的时候，一般还会问你是否不存在满足该信息的数值，如果是输出no，那么我们就可以在找到假设的数值之后，再去过一遍给的信息，判定是否信息和数值对的上。这是一个很好的处理方法和思路。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define sz(a) int(a.size())
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define chu(x) cout<<"["<<#x<<" "<<(x)<<"]"<<endl
#define du3(a,b,c) scanf("%d %d %d",&(a),&(b),&(c))
#define du2(a,b) scanf("%d %d",&(a),&(b))
#define du1(a) scanf("%d",&(a));
using namespace std;
typedef long long ll;
ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;}
ll lcm(ll a, ll b) {return a / gcd(a, b) * b;}
ll powmod(ll a, ll b, ll MOD) {a %= MOD; if (a == 0ll) {return 0ll;} ll ans = 1; while (b) {if (b & 1) {ans = ans * a % MOD;} a = a * a % MOD; b >>= 1;} return ans;}
void Pv(const vector<int> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%d", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}
void Pvl(const vector<ll> &V) {int Len = sz(V); for (int i = 0; i < Len; ++i) {printf("%lld", V[i] ); if (i != Len - 1) {printf(" ");} else {printf("\n");}}}

inline void getInt(int* p);
const int maxn = 1000010;
const int inf = 0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
set<int> st;
int y = 0;
int a[maxn];
int ans1 = 1e9;
int n;
int main()
{
    //freopen("D:\\code\\text\\input.txt","r",stdin);
    //freopen("D:\\code\\text\\output.txt","w",stdout);
    gbtb;
    cin >> n;
    repd(i, 1, n)
    {
        cin >> a[i];
    }
    if (n == 1)
    {
        cout << "YES" << endl;
        cout << ans1 << " " << 1 << endl;
        return 0;
    }

    repd(i, 2, n)
    {
        st.insert(abs(a[i] - a[i - 1]));
        y = max(y, abs(a[i] - a[i - 1]));
        if (a[i] == a[i - 1])
        {
            st.insert(10);
            st.insert(11);
            st.insert(14);
            break;
        }
    }
    if (st.size() > 2)
    {
        cout << "NO" << endl;
    } else
    {
        if (st.size() == 2 && (*st.begin()) != 1)
        {
            cout << "NO" << endl;
        }
        else if (y == 1)
        {
            cout << "YES" << endl;
            cout << ans1 << " " << 1 << endl;
        } else
        {
            int isok = 1;

            repd(i, 1, n - 1)
            {
                int cha = a[i + 1] - a[i];
                if ((a[i] % y) == 0 && cha == 1)
                {
                    isok = 0;
                    break;
                } else if ((a[i] % y) == 1 && cha == -1)
                {
                    isok = 0;
                    break;
                }
            }
            if (isok)
            {
                cout << "YES" << endl;
                cout << ans1 << " " << y << endl;
            } else
            {
                cout << "NO" << endl;
            }
        }
    }
    return 0;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '0');
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 - ch + '0';
        }
    }
    else {
        *p = ch - '0';
        while ((ch = getchar()) >= '0' && ch <= '9') {
            *p = *p * 10 + ch - '0';
        }
    }
}