《算法问题实战策略》-chaper13-数值分析

这一章节主要介绍我们在进行数值分析常用的二分、三分和一个近似求解区间积分的辛普森法。

首先介绍二分。

其实二分的思想很好理解并且笔者在之前的一些文章中也有所渗透，对于二次函数甚至单元高次函数的零点求解、线段树还有《algorithm puzzle》当中的“切割钢条”问题，都是基于二分思想。

下面我们通过具体的问题来应用二分这种数值分析的策略。

Ex1：按揭贷款

以P%的年利率借贷N元后，在M个月内，以每月还C元的方式还贷。贷款期限内，按照如下形式计算贷款余额。

(1)    贷款余额从余额N元开始。

(2)    美国一个月，贷款余额会增加一个月的利息，月利率为(P/12)%。

(3)    增加利息后，从贷款余额中扣除当月的还款项。

分析：我们从较为抽象化的角度来建立一个数学模型，这道问题M，P，N，C等输入数据相当于是自变量，而还贷过程相当于是个函数机制，M月后的借贷余额便是因变量。

对于函数的这三要素，我们都是知道的，那么我们可以将问题转化成在满足因变量≤0的情况下，求解C的最小值。

如果我们想尝试利用数学方法，会发现我们虽然了解函数机制，但是我们难以列出其表达式，因此这里我们基于自变量C的解区间，进行二分搜索，而这个过程恰恰基于函数机制和因变量(函数余额)的范围限制。

简单的参考代码如下：

  #include<cstdio>

using namespace std;

double balance(double amount , int duration , double rates , double monthlypayment)//求解每月还贷monthlypayment元，duration个月后的贷款余额。

{

    double balance = amount;//贷款余额初始化

    for(int i = ;i < duration;i++)

    {

        balance *= (1.0 + (rates/12.0)/100.0);//这里涉及简单的还贷机制，我们将其理解为每月底涨息后还贷

        balance -= monthlypayment;

    }

    return balance;

}

double payment(double amount , int duration , double rates)

{

    double l = ;//每月还贷可行解的区间，基于这道问题的特殊情景(区间右端点一定可行，这与这个函数最后return的变量呼应)，解区间分布情况是(,]

    double r = amount*(1.0 + (rates/12.0)/100.0);

    double mid;

    for(int i = ;i < ;i++)

    {

         mid = (r + l)/2.0;

        if(balance(amount , duration , rates , mid) <= )

                r = mid;

        else

                l = mid;

    }

    return r;

}

int main()

{

    double amount , rates;

    int duration;

    printf("Input amount,rates and duration:");

    scanf("%lf %lf %d",&amount,&rates,&duration);

    printf("the lowest monthlypayment: %llf",payment(amount,duration,rates));

}

下面我们开始介绍三分。

其实所谓三分，如果百度一下，会发现在百度百科里它是一种“哲学形态”出现的，并且被称为典型的中国思维，即在解决问题的时候基于西方所谓“二分”的思维，将正反对立双方进行统一，形成事物的“第三面”。

但是我们这里并不从哲学的角度去看待三分，而是从数值分析的角度去看待三分，即将其看成一种筛选解的搜索方式。

对于一个函数f(x)，考察其在[lo,hi]上的性质。

零点：这个我们都很熟悉，利用二分法可以快速求解，但是为什么要在这里介绍呢？是为了将其与三分进行区别和联系。

极值点：

为了讨论的方便和算法的简便，我们统一一下讨论的函数，它在区间[lo,hi]上先严格递增后严格递减，存在一个极大值点。

想一想，如果想用这种基于解区间进行搜索的办法，利用二分能否能够实现呢？不能。因为对于零点，我们所基于的解空间的两端仿佛就是走了两个极端，一个大于0一个小于0，这导致零点必然会落在这之间，并且二分区间之后依然能够容易得得到更小的解区间，而对于极值的情况，显然解区间的两个端点要么都小于极值点的，因此这样你二分是无法选择下一个更下的解区间，这就使得搜索过程变得没了意义。

那应该怎么处理呢？这就很自然的引出了今天的主角——三分法。我们将区间[lo,hi]三等分(三等分点怎么求就不必我多说了)，无非会出现如下的两种情况：

(1)左三等分点对应的函数值较大，那么我们可以很肯定的说，三等分区间之中最右边的区间一定不会有极值，因为假设最右边的区间上还有极值点，按照我们先前的定义，极值点的左侧是严格递增的，这与事实相悖。

(2)同理，如果右三等分点对应的函数值较大，我们能够排除三等分区间的最左侧的区间。

而类似于二分搜索法，对于在实数区间上的三分搜索，我们默认进行100次三分之后终止，得到近似解。

简单的函数代码如下。

double f(double x);//求解函数值f(x)

double ternary(double lo , double hi)

{

    double a  = (*lo + hi)/;//左三等分点

    double b  = (lo + *hi)/;//右三等分点

    for(int i = ;i < ;i++)//三分100次终止

    {

      if(f(a) < f(b))   lo = a;

      else              hi = b;

    }

    return (lo + hi)/;

}

辛普森法：

所谓辛普森法，即是在求解函数f(x)在[a,b]区间上的积分是，将x = a、b、(a + b)/2三点视作抛物线上的三个点，这样我们通过简单的定积分运算，可以得到一个公式，即：

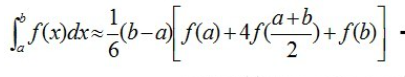
但是，上面提到的“将三点视为抛物线上的三个点”这种近似处理显然是要付出相应的代价的，这里在微积分的层面就要用到极限的思维方法，但是在这里我们从计算机编程的角度来看，我们基于二分来设计一个递归过程来“偿还”这种代价。

假设我们求得了[a,b]上的积分，我们分别二分区间得到[a,(a+b)/2]、[(a+b)/2,b]并用相同的办法求出这两个区间上的积分值，限制二者的和与先前求得的积分误差在1e-10以内，则表明认为符合了我们上文提到的“近似”处理，否自，我们继续二分区间，形成一个递归过程，知道满足误差的限定为止。

我们通过一个具体的题目来实现这个算法流程。(Problem source : hdu 1724)

给出一个椭圆方程，的两个参数a、b和一个区间[c,d]的左右端点，请求解直线x = c，x=d和椭圆围成的面积。

简单的参考代码如下：

#include <iostream>
#include <math.h>
#include<cstdio>
using namespace std;

const double esp = 1e-;
double a,b;

double f(double x)//被积函数
{
    return b * sqrt(1.0-(x*x)/(a*a));
}

double simpson(double l,double r)
{
    return (f(l)+*f((l+r)/2.0)+f(r))/6.0*(r-l);
}

double integral(double l,double r)
{
    double mid = (l+r)/2.0;
    double res = simpson(l,r);
    if (fabs(res-simpson(l,mid)-simpson(mid,r)) < esp)
        return res;
    else
        return integral(l,mid) + integral(mid,r);
}
int main()
{
    int T;
    double l,r;
    cin >> T;
    while (T--)
    {
        cin >> a >> b >> l >> r;
        printf("%.3lf\n",*integral(l,r));
    }
    return ;
}