Java经典算法汇总之冒泡排序

冒泡排序基本思想：在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

原理：比较两个相邻的元素，将值大的元素交换至右端。

思路：依次比较相邻的两个数，将小数放在前面，大数放在后面。即在第一趟：首先比较第1个和第2个数，将小数放前，大数放后。然后比较第2个数和第3个数，将小数放前，大数放后，如此继续，直至比较最后两个数，将小数放前，大数放后。重复第一趟步骤，直至全部排序完成。

举例说明：要排序数组：int[]arr={6,3,8,2,9,1};

第一趟排序：

　　　　第一次排序：6和3比较，6大于3，交换位置：368291

　　　　第二次排序：6和8比较，6小于8，不交换位置：368291

　　　　第三次排序：8和2比较，8大于2，交换位置：362891

　　　　第四次排序：8和9比较，8小于9，不交换位置：362891

　　　　第五次排序：9和1比较：9大于1，交换位置：362819

　　　　第一趟总共进行了5次比较， 排序结果： 362819

---------------------------------------------------------------------

第二趟排序：

　　　　第一次排序：3和6比较，3小于6，不交换位置：362819

　　　　第二次排序：6和2比较，6大于2，交换位置：326819

　　　　第三次排序：6和8比较，6大于8，不交换位置：326819

　　　　第四次排序：8和1比较，8大于1，交换位置：326189

　　　　第二趟总共进行了4次比较， 排序结果： 326189

---------------------------------------------------------------------

第三趟排序：

　　　　第一次排序：3和2比较，3大于2，交换位置：236189

　　　　第二次排序：3和6比较，3小于6，不交换位置：236189

　　　　第三次排序：6和1比较，6大于1，交换位置：231689

　　　　第二趟总共进行了3次比较， 排序结果： 231689

---------------------------------------------------------------------

第四趟排序：

　　　　第一次排序：2和3比较，2小于3，不交换位置：231689

　　　　第二次排序：3和1比较，3大于1，交换位置：213689

　　　　第二趟总共进行了2次比较， 排序结果： 213689

---------------------------------------------------------------------

第五趟排序：

　　　　第一次排序：2和1比较，2大于1，交换位置：123689

　　　　第二趟总共进行了1次比较， 排序结果： 123689

---------------------------------------------------------------------

最终结果：123689

---------------------------------------------------------------------

由此可见：N个数字要排序完成，总共进行N-1趟排序，每i趟的排序次数为(N-i)次，所以可以用双重循环语句，外层控制循环多少趟，内层控制每一趟的循环次数，即

?

1 2 3 4 5 6 7

for(int i=1;i<arr.length-1;i++){     for(int j=1;j<arr.length-1-i;j++){     //交换位置   }

冒泡排序的优点：每进行一趟排序，就会少比较一次，因为每进行一趟排序都会找出一个较大值。如上例：第一趟比较之后，排在最后的一个数一定是最大的一个数，第二趟排序的时候，只需要比较除了最后一个数以外的其他的数，同样也能找出一个最大的数排在参与第二趟比较的数后面，第三趟比较的时候，只需要比较除了最后两个数以外的其他的数，以此类推……也就是说，没进行一趟比较，每一趟少比较一次，一定程度上减少了算法的量。

用时间复杂度来说：

　　1.如果我们的数据正序，只需要走一趟即可完成排序。所需的比较次数和记录移动次数均达到最小值，即：Cmin=n-1;Mmin=0;所以，冒泡排序最好的时间复杂度为O(n)。

　　2.如果很不幸我们的数据是反序的，则需要进行n-1趟排序。每趟排序要进行n-i次比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值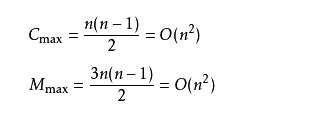：冒泡排序的最坏时间复杂度为：O(n2)。

综上所述：冒泡排序总的平均时间复杂度为：O(n2)。

代码实现：

?

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

/*  * 冒泡排序  */ public class BubbleSort { 　　public static void main(String[] args) { 　　　　int[] arr={6,3,8,2,9,1}; 　　　　System.out.println("排序前数组为："); 　　　　for(int num:arr){ 　　　　　　System.out.print(num+" "); 　　　　} 　　　　for(int i=1;i<arr.length;i++){//外层循环控制排序趟数 　　　　　　for(int j=1;j<arr.length-i;j++){//内层循环控制每一趟排序多少次 　　　　　　　　if(arr[j-1]>arr[j]){ 　　　　　　　　　　int temp=arr[j]; 　　　　　　　　　　arr[j]=arr[j-1]; 　　　　　　　　　　arr[j-1]=temp; 　　　　　　　　} 　　　　　　} 　　　　} 　　　　System.out.println(); 　　　　System.out.println("排序后的数组为：");  　　　　for(int num:arr){  　　　　　　System.out.print(num+" ");  　　　　} 　　}  }