[最短路][部分转] P1073 最优贸易

题目描述

C 国有 n 个大城市和 m 条道路，每条道路连接这 n 个城市中的某两个城市。任意两个

城市之间最多只有一条道路直接相连。这 m 条道路中有一部分为单向通行的道路，一部分

为双向通行的道路，双向通行的道路在统计条数时也计为 1 条。

C 国幅员辽阔，各地的资源分布情况各不相同，这就导致了同一种商品在不同城市的价

格不一定相同。但是，同一种商品在同一个城市的买入价和卖出价始终是相同的。

商人阿龙来到 C 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息

之后，便决定在旅游的同时，利用商品在不同城市中的差价赚回一点旅费。设 C 国 n 个城

市的标号从 1~ n，阿龙决定从 1 号城市出发，并最终在 n 号城市结束自己的旅行。在旅游的

过程中，任何城市可以重复经过多次，但不要求经过所有 n 个城市。阿龙通过这样的贸易方

式赚取旅费：他会选择一个经过的城市买入他最喜欢的商品――水晶球，并在之后经过的另

一个城市卖出这个水晶球，用赚取的差价当做旅费。由于阿龙主要是来 C 国旅游，他决定

这个贸易只进行最多一次，当然，在赚不到差价的情况下他就无需进行贸易。

假设 C 国有 5 个大城市，城市的编号和道路连接情况如下图，单向箭头表示这条道路

为单向通行，双向箭头表示这条道路为双向通行。

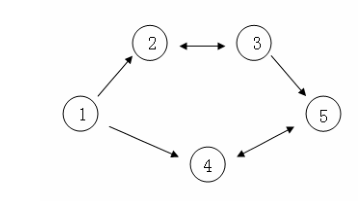
假设 1~n 号城市的水晶球价格分别为 4，3，5，6，1。

阿龙可以选择如下一条线路：1->2->3->5，并在 2 号城市以 3 的价格买入水晶球，在 3

号城市以 5 的价格卖出水晶球，赚取的旅费数为 2。

阿龙也可以选择如下一条线路 1->4->5->4->5，并在第 1 次到达 5 号城市时以 1 的价格

买入水晶球，在第 2 次到达 4 号城市时以 6 的价格卖出水晶球，赚取的旅费数为 5。

现在给出 n 个城市的水晶球价格，m 条道路的信息（每条道路所连接的两个城市的编号

以及该条道路的通行情况）。请你告诉阿龙，他最多能赚取多少旅费。

输入输出格式

输入格式：

第一行包含 2 个正整数 n 和 m，中间用一个空格隔开，分别表示城市的数目和道路的

数目。

第二行 n 个正整数，每两个整数之间用一个空格隔开，按标号顺序分别表示这 n 个城

市的商品价格。

接下来 m 行，每行有 3 个正整数，x，y，z，每两个整数之间用一个空格隔开。如果 z=1，

表示这条道路是城市 x 到城市 y 之间的单向道路；如果 z=2，表示这条道路为城市 x 和城市

y 之间的双向道路。

输出格式：

输出文件 trade.out 共 1 行，包含 1 个整数，表示最多能赚取的旅费。如果没有进行贸易，

则输出 0。

输入输出样例

输入样例#1：

输出样例#1：

说明

【数据范围】

输入数据保证 1 号城市可以到达 n 号城市。

对于 10%的数据，1≤n≤6。

对于 30%的数据，1≤n≤100。

对于 50%的数据，不存在一条旅游路线，可以从一个城市出发，再回到这个城市。

对于 100%的数据，1≤n≤100000，1≤m≤500000，1≤x，y≤n，1≤z≤2，1≤各城市

水晶球价格≤100。

NOIP 2009 提高组第三题

说明

------------------------------------------------------

Oops! 你的分析出现了一些问题,需要在这儿省略.

已完成 1% : (

请查阅代码: 0x23333333或联系版主

------------------------------------------------------

 #include<cstdio>
 #include<iostream>
 #include<vector>
 #include<algorithm>
 using namespace std;
 #define N 100002
 int n,m,s[N],maxn[N],minn[N],ans;
 vector<int>a[N],b[N];
 void dfs1(int g ,int h){//g为城市编号，h为当前城市的价格
     minn[g]=min(h,minn[g]);//因为双向边可以来回，买价可以更低
     ;i<a[g].size();i++)
         if(h<minn[a[g][i]])
             dfs1(a[g][i],min(s[a[g][i]],h));
 }
 void dfs2(int g ,int h){//同理
     maxn[g]=max(h,maxn[g]);
     ;i<b[g].size();i++)
         if(h>maxn[b[g][i]])
             dfs2(b[g][i],max(s[b[g][i]],h));
 }
 int main(){
     /*
         模版转自:http://www.cnblogs.com/shenben/p/5634839.html
     */
     scanf("%d%d",&n,&m);
     ;i<=n;i++)
         scanf("%d",s+i);//(dR)每个城市的价格
     ,x,y,z;i<=m;i++){
         scanf("%d%d%d",&x,&y,&z);
         )
             a[x].push_back(y),b[y].push_back(x);//单边
         else
             a[x].push_back(y),a[y].push_back(x),b[x].push_back(y),b[y].push_back(x);//双边
     }
     ;i<=n;i++)
         maxn[i]=-1e9,minn[i]=1e9;
     dfs1(,s[]);//低价买
     dfs2(n,s[n]);//高价卖
     ;i<=n;i++)//类似题: 我记得有来着
         if(maxn[i]!=-1e9&&minn[i]!=1e9)
             ans=max(ans,maxn[i]-minn[i]);
     printf("%d\n",ans);
     ;
 }

代码