Floyd-Warshall 算法-- 最短路径（适合节点密集的图）

 由于此算法时间复杂度为O(V³）。大多数情况下不如迪杰斯特拉算法的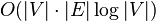。迪杰斯特拉算法适合于节点疏散的图。

 演示样例图例如以下：

 

 

Step 1 创建节点与边的最短路径结果表（直接可达关系）。数值表示距离。INF表示不可达

	1	2	3	4
1	0	8	INF	1
2	INF	0	1	INF
3	4	INF	0	INF
4	INF	2	9	0

Step2 找出全部经过1的路径。更新两点间的最短路径

经过1的路径即全部入度和出度路径的组合，总数为入度×出度：

 

 

经过1路径为：

第一条，3-1-2

眼下MIN(3->2)为INF，而MIN(3->1->2)=4+8=12 因此MIN(3->2)为12，由于2有更新，故要递归更新全部从3到2可达点的最短路径。而2可达点仅仅有3，MIN(3->3)为0，因此不须要更新。

第二条，3-1-4

眼下MIN(3->4)为INF，而MIN(3->1->4)=4+1=5，因此MIN(3->4)为5，由于4有更新，故要递归更新全部从3到4的全部可达点的最短路径，而4的可达点为3和2：

MIN(3->3)=0，MIN(3->2)=MIN(3->1->2)=12  > MIN(3->1->4->2)= 7。因此MIN(3->2)=7

找出全部经过1路径的结果为：

 

 

 

	1	2	3	4
1	0	8	INF	1
2	INF	0	1	INF
3	4		0
4	INF	2	9	0

Step3 找出全部经过2的路径

 

第1条，1->2->3

由于MIN(1->3)为INF，而MIN(1->2->3)为9。因此MIN(1->3)为9，由于3有更新，所以须要递归更新全部从1到3可达点的最短路径，由于3的可达点为1，而MIN(1->1)不须要更新，为0。如今看第二条路径：

第二条。4->2->3

因此MIN(4->3)为9，而MIN(4->2->3)为3。因此MIN(4->3)=3，由于3有更新，须要递归更新从4到3可达点的最短路径，由于3的可达点为1，而MIN(4->1)为INF，MIN(4->2->3->1)为7。因此MIN(4->1)为7。由于1有更新，继续递归，1的可达点为4和2，MIN(4->4)保持0；眼下MIN(4->2)为2，而MIN(4->2->3->1->2)=2+1+4+8=15大于2。因此不须要更新。

找出全部经过2的路径后，结果为：

	1	2	3	4
1	0	8		1
2	INF	0	1	INF
3	4	7	0	5
4		2		0

Step4 找出全部经过3的路径

第1条。4->3->1

MIN(4->1)为7。而MIN(4->3->1)为13。因此不须要更新

第二条，2->3->1

由于MIN(2->1)为INF，而MIN(2->3->1)为5。因此须要更新MIN(2->1)为5。

由于更新了1，因此须要更新全部从2到1可达点的路径，1的可达点为4和2，MIN(2->2)不须要更新；眼下MIN(2->4)为INF。而MIN(2->3->1->4)为6。因此MIN(2->4)为6。由于更新了4，因此须要递归更新从2到4可达点的路径，4可达点为2和3，MIN(2->2)为0；MIN(2->3)为1小于MIN(2->3->1->4->3)=1+4+1+9=15。故也不须要更新。

所以经过这一步，结果表为：

 

 

 

	1	2	3	4
1	0	8	9	1
2	5	0	1	6
3	4	7	0	5
4	7	2	3	0

最后，找出经过4的路径。

 

watermark/2/text/aHR0cDovL2Jsb2cuY3Nkbi5uZXQv/font/5a6L5L2T/fontsize/400/fill/I0JBQkFCMA==/dissolve/70/gravity/Center" alt="" />

第一条。1->4->2

MIN(1->2)为8，而MIN(1->4->2)为3，因此MIN(1->2)更新为3，由于更新了2。故须要更新全部从1到2可达点的最短路径，2的可达点为3。MIN(1->3)眼下为9。而MIN(1->4->2->3)为4，因此MIN(1->3)更新为4。由于更新了3。故递归更新全部从1到3可达点的最短路径，3的可达点为1，而MIN(1->1)不须要更新保持为0。

第二条，1->4->3

MIN(1->3)为4，而MIN(1->4->3)为10。因此不须要更新。

所以终于结果为：

	1	2	3	4
1	0			1
2	5	0	1	6
3	4	7	0	5
4	7	2	3	0