poj1179 区间dp（记忆化搜索写法）有巨坑！

http://poj.org/problem?id=1179

Description

Polygon is a game for one player that starts on a polygon with N vertices, like the one in Figure 1, where N=4. Each vertex is labelled with an integer and each edge is labelled with either the symbol + (addition) or the symbol * (product). The edges are numbered
from 1 to N. 




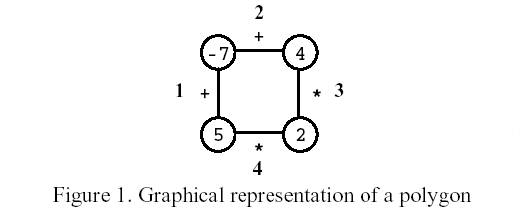
On the first move, one of the edges is removed. Subsequent moves involve the following steps: 

�pick an edge E and the two vertices V1 and V2 that are linked by E; and 

�replace them by a new vertex, labelled with the result of performing the operation indicated in E on the labels of V1 and V2. 

The game ends when there are no more edges, and its score is the label of the single vertex remaining. 



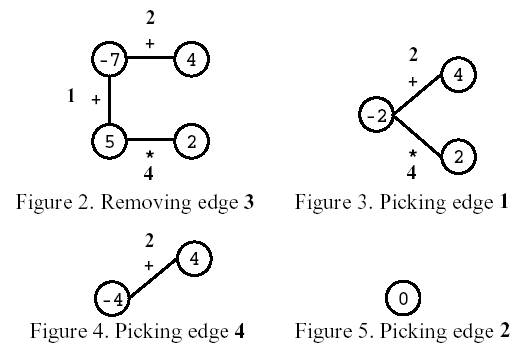
Consider the polygon of Figure 1. The player started by removing edge 3. After that, the player picked edge 1, then edge 4, and, finally, edge 2. The score is 0. 




Write a program that, given a polygon, computes the highest possible score and lists all the edges that, if removed on the first move, can lead to a game with that score. 

Input

Your program is to read from standard input. The input describes a polygon with N vertices. It contains two lines. On the first line is the number N. The second line contains the labels of edges 1, ..., N, interleaved with the vertices' labels (first that of
the vertex between edges 1 and 2, then that of the vertex between edges 2 and 3, and so on, until that of the vertex between edges N and 1), all separated by one space. An edge label is either the letter t (representing +) or the letter x (representing *). 



3 <= N <= 50 

For any sequence of moves, vertex labels are in the range [-32768,32767]. 

Output

Your program is to write to standard output. On the first line your program must write the highest score one can get for the input polygon. On the second line it must write the list of all edges that, if removed on the first move, can lead to a game with that
score. Edges must be written in increasing order, separated by one space.

Sample Input

4
t -7 t 4 x 2 x 5

Sample Output

33
1 2

/**
hdu 1179  区间dp（记忆化搜索写法）
题目大意：给定一个n个节点的环，环的每条边代表+或者*。问最開始把哪条边去掉。剩下的做运算能够得到最大的表达式的值
解题思路：枚举去掉n条边的随意一条，然后区间dp来写。值得一提的是两个最小的负数相乘就会是最大的值，所以我们不能仅仅维护最大值
          同一时候也须要维护最小值。

坑啊，这个陷阱太厉害了
*/
#include <stdio.h>
#include <string.h>
#include <iostream>
#include <algorithm>
using namespace std;

int num[105],sym[105],n;
int dpmin[155][155],dpmax[155][155];
int vismin[155][155],vismax[155][155];
int MAX(int i,int j);
int MIN(int i,int j);

int MAX(int x,int y)
{
    if(vismax[x][y])return dpmax[x][y];
    vismax[x][y]=1;
    if(y==x)
    {
        dpmax[x][y]=num[x];
        return dpmax[x][y];
    }
    dpmax[x][y]=-1000000007;
    for(int i=x;i<y;i++)
    {
        int l=MAX(x,i);
        int ll=MIN(x,i);
        int r=MAX(i+1,y);
        int rr=MIN(i+1,y);
        if(sym[i+1])
        {
            dpmax[x][y]=max(dpmax[x][y],l+r);
        }
        else
        {
            int ans=l*r;
            ans=max(ans,l*rr);
            ans=max(ans,ll*r);
            ans=max(ans,ll*rr);
            dpmax[x][y]=max(dpmax[x][y],ans);
        }
    }
    return dpmax[x][y];
}

int MIN(int x,int y)
{
    if(vismin[x][y])return dpmin[x][y];
    vismin[x][y]=1;
    if(y==x)
    {
        dpmin[x][y]=num[x];
        return dpmin[x][y];
    }
    dpmin[x][y]=1000000007;
    for(int i=x;i<y;i++)
    {
        int l=MAX(x,i);
        int ll=MIN(x,i);
        int r=MAX(i+1,y);
        int rr=MIN(i+1,y);
        if(sym[i+1])
        {
            dpmin[x][y]=min(dpmin[x][y],ll+rr);
        }
        else
        {
            int ans=l*r;
            ans=min(ans,l*rr);
            ans=min(ans,ll*r);
            ans=min(ans,ll*rr);
            dpmin[x][y]=min(dpmin[x][y],ans);
        }
    }
    return dpmin[x][y];
}
int main()
{
    while(~scanf("%d%*c",&n))
    {
        for(int i=0;i<n;i++)
        {
            char ch;
            scanf("%c %d%*c",&ch,&num[i]);
            num[i+n]=num[i];
            sym[i+n]=sym[i]=(ch=='t');
        }
        memset(dpmin,0,sizeof(dpmin));
        memset(dpmax,0,sizeof(dpmax));
        memset(vismin,0,sizeof(vismin));
        memset(vismax,0,sizeof(vismax));
        int maxx=-1000000007;
        int sum[55],id;
        for(int i=0;i<n;i++)
        {
            int ans=MAX(i,i+n-1);
           /** for(int j=i;j<=i+n-1;j++)
            {
                printf("%d %c ",num[j],sym[j+1]==0?'*':'+');
            }
            printf("\n%d\n",ans);*/
            if(ans>maxx)
            {
                maxx=ans;
                id=0;
                sum[id++]=i+1;
            }
            else if(ans==maxx)
            {
                sum[id++]=i+1;
            }
        }
        printf("%d\n",maxx);
        for(int i=0;i<id;i++)
        {
            printf(i==id-1?"%d\n":"%d ",sum[i]);
        }
    }
    return 0;
}