A1146. Topological Order

This is a problem given in the Graduate Entrance Exam in 2018: Which of the following is NOT a topological order obtained from the given directed graph? Now you are supposed to write a program to test each of the options.

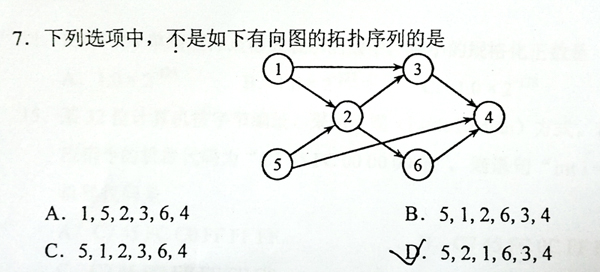
Input Specification:

Each input file contains one test case. For each case, the first line gives two positive integers N (≤ 1,000), the number of vertices in the graph, and M (≤ 10,000), the number of directed edges. Then M lines follow, each gives the start and the end vertices of an edge. The vertices are numbered from 1 to N. After the graph, there is another positive integer K (≤ 100). Then K lines of query follow, each gives a permutation of all the vertices. All the numbers in a line are separated by a space.

Output Specification:

Print in a line all the indices of queries which correspond to "NOT a topological order". The indices start from zero. All the numbers are separated by a space, and there must no extra space at the beginning or the end of the line. It is graranteed that there is at least one answer.

Sample Input:

6 8
1 2
1 3
5 2
5 4
2 3
2 6
3 4
6 4
5
1 5 2 3 6 4
5 1 2 6 3 4
5 1 2 3 6 4
5 2 1 6 3 4
1 2 3 4 5 6

Sample Output:

3 4

#include<iostream>
#include<cstdio>
using namespace std;
int G[][] = {}, dele[] = {};
int N, M, K;
int main(){
    scanf("%d%d", &N, &M);
    for(int i = ; i < M; i++){
        int v1, v2;
        scanf("%d%d", &v1, &v2);
        G[v1][v2] = ;
    }
    scanf("%d", &K);
    int ans[], pt = ;
    for(int i = ; i < K; i++){
        fill(dele, dele + , );
        int isTopl = ;
        for(int j = ; j <= N; j++){
            int v;
            int tag = ;
            scanf("%d", &v);
            for(int k = ; k <= N; k++){
                if(dele[k] ==  && G[k][v] != ){
                    tag = ;
                    break;
                }
            }
            if(tag == ){
                isTopl = ;
            }else{
                dele[v] = ;
            }
        }
        if(isTopl == ){
            ans[pt++] = i;
        }
    }
    for(int i = ; i < pt; i++){
        if(i == pt - )
            printf("%d", ans[i]);
        else printf("%d ", ans[i]);
    }
    cin >> N;
}

总结：

1、题意：给出一个有向图，检验给出的序列是否是拓扑排序。

2、拓扑排序要求每次删除一个入度为0的节点。