Kruskal算法求最小生成树 笔记与思路整理

整理一下前一段时间的最小生成树的算法。（其实是刚弄明白

Kruskal其实算是一种贪心算法。先将边按权值排序，每次选一条没选过的权值最小边加入树，若加入后成环就跳过。

先贴张图做个示例。

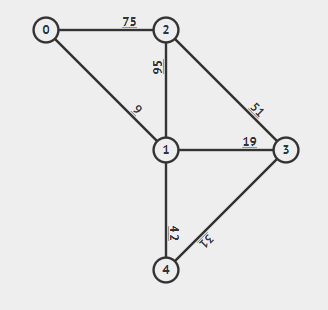（可视化均来自VisuAlgo）

1、邻接链表按权值排序后（可以直接写个cmp，sort()结构体）：

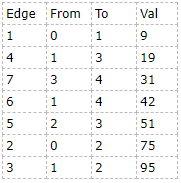
2、依次选边，若成环则跳过，否则加入最小生成树并计数。

　　这里判断是否成环用的是并查集：如果新加入的边两个端点在同一个集合中，就说明已经有一条路径联通这两个端点。

3、重复2，直到加入了n-1条边或遍历完成（无最小生成树）。

选取1号、4号、7号后：

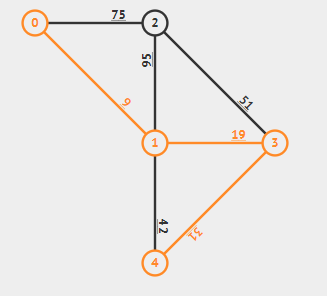
选取6号（1--4），成环，跳过；

加入5号（2--3），达到n-1条，最小生成树形成。

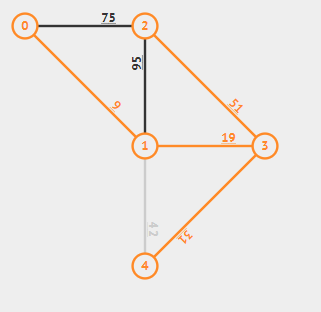
代码实现：

#include <bits/stdc++.h>
#define maxn 100010
using namespace std;

struct edge{
    int from, to, val;
};
edge tree[maxn];
bool cmp(const edge &a, const edge &b){
    return a.val < b.val;
}
int m, n, father[maxn], rslt = ;
bool possible = true;

int get_father(int x){
    if(father[x] == x) return x;
    return father[x] = get_father(father[x]);
}
void kruskal(){
    int f1, f2, cnt = ;
    for(int i=; i<=n; i++){
        father[i] = i;
    }
    for(int i=; i<=m; i++){
        f1 = get_father(tree[i].from);
        f2 = get_father(tree[i].to);
        if(f1 != f2){
            rslt += tree[i].val;
            father[f1] = f2;
            if(++cnt == n-){
                return;
            }
        }
    }
    possible = false;
    cout << "Impossible!";
    return;
}

int main(){
    cin >> n >> m;
    for(int i=; i<=m; i++){
        cin >> tree[i].from >> tree[i].to >> tree[i].val;
    }
    sort(tree+, tree+m+, cmp);
    kruskal();
    if(possible) cout << rslt;
    return ;
}