洛谷 P1939 【模板】矩阵加速（数列） 解题报告

P1939 【模板】矩阵加速（数列）

题目描述

a[1]=a[2]=a[3]=1

a[x]=a[x-3]+a[x-1] (x>3)

求a数列的第n项对1000000007（10^9+7）取余的值。

输入输出格式

输入格式：

第一行一个整数T，表示询问个数。

以下T行，每行一个正整数n。

输出格式：

每行输出一个非负整数表示答案。

说明

对于30%的数据 n<=100；

对于60%的数据 n<=2*10^7；

对于100%的数据 T<=100，n<=2*10^9；

---

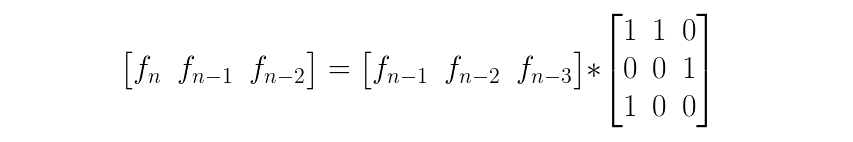
直接套矩阵快速幂即可

---

Code：

#include <cstdio>
#include <cstring>
#define ll long long
const ll mod=1e9+7;
int n,t;
struct matrix
{
    ll dx[4][4];
    matrix()
    {
        memset(dx,0,sizeof(dx));
    }
    matrix friend operator *(matrix n1,matrix n2)
    {
        matrix n3;
        for(int i=1;i<=3;i++)
            for(int j=1;j<=3;j++)
                for(int k=1;k<=3;k++)
                    n3.dx[i][j]=(n3.dx[i][j]+n1.dx[i][k]*n2.dx[k][j])%mod;
        return n3;

    }
}f,d,ans;
void quick(int k)
{
    while(k)
    {
        if(k&1)
            f=f*d;
        d=d*d;
        k>>=1;
    }
}
void init()
{
    ans.dx[1][1]=1,ans.dx[1][2]=1,ans.dx[1][3]=1;
    ans.dx[2][1]=0,ans.dx[2][2]=0,ans.dx[2][3]=0;
    ans.dx[3][1]=0,ans.dx[3][2]=0,ans.dx[3][3]=0;
    f.dx[1][1]=1,f.dx[1][2]=0,f.dx[1][3]=0;
    f.dx[2][1]=0,f.dx[2][2]=1,f.dx[2][3]=0;
    f.dx[3][1]=0,f.dx[3][2]=0,f.dx[3][3]=1;
    d.dx[1][1]=1,d.dx[1][2]=1,d.dx[1][3]=0;
    d.dx[2][1]=0,d.dx[2][2]=0,d.dx[2][3]=1;
    d.dx[3][1]=1,d.dx[3][2]=0,d.dx[3][3]=0;
}
void work()
{
    scanf("%d",&t);
    while(t--)
    {
        init();
        scanf("%d",&n);
        if(n>3)
        {
            quick(n-3);
            ans=ans*f;
            printf("%d\n",ans.dx[1][1]);
        }
        else
            printf("1\n");
    }
}
int main()
{
    work();
    return 0;
}

---

2017.7.2