【C++】神秘-希尔排序

插入排序
希尔排序
- 希尔排序的优点
  - - 时间复杂度
- 希尔排序的思想

插入排序

在待排序的元素中，假设前k个元素已有序，现将第k+1个元素插入到前面已经排好的序列中，使得前k个元素有序。

按照此法对所有元素进行插入，直到整个序列有序。

但我们并不能确定待排元素中究竟哪一部分是有序的。，

所以我们一开始只能认为第一个元素是有序的，依次将其后面的元素插入到这个有序序列中来，直到整个序列有序为止。

↑↑↑黑色圈住的数字表示要插入到前面序列的数字

希尔排序

讲完插入排序，就该讲我们的重点了。

希尔排序是一种改进的插入排序算法，也被称为缩小增量排序。

它通过将待排序序列分割成多个子序列来进行排序，然后逐步缩小子序列的长度，最终使整个序列变为有序。

希尔排序的核心思想是将相距某个增量的元素组成一个子序列，对子序列进行插入排序。

然后逐步减小增量，重复上述过程，直到增量为1时，完成最后一次插入排序，使整个序列成为有序的。

希尔排序的优点

效率较高：对于大规模数据集，希尔排序通常比简单插入排序更快，特别是在处理近乎有序的数据时，由于跳跃式的比较和交换，效率提升显著。
灵活性：希尔排序通过调整间隔序列来适应不同类型的数据分布，这使得它在某些情况下能获得更好的性能，尽管没有一种固定的间隔序列适合所有场景。
稳定性：虽然希尔排序本质上不是稳定的排序算法，但在某些实现版本中，如果对相等元素进行特殊处理，可以保持相对位置不变，表现为某种形式的稳定性。
易于理解：作为一种改进的插入排序，希尔排序的原理相对直观，容易学习和实现。

然而，希尔排序的主要缺点在于它的时间复杂度依赖于所选的间隔序列，不稳定性和最坏情况下的效率不高可能会限制它在一些高并发环境下的使用。

因此，在实际应用中需要权衡性能和代码实现复杂性。

时间复杂度

希尔排序的时间复杂度取决于增量序列的选取， 一般最好情况下为O(nlogn)，最坏情况下为O(n^2)。

希尔排序是 不稳定的排序算法 ，即可能改变相同元素的原始顺序。

希尔排序的思想

希尔排序也被称为缩小增量排序。

其基本思想是将待排序的元素按照一定的间隔分组，对每组使用插入排序算法进行排序，

然后逐步缩小间隔，再进行排序，直至间隔为1时进行最后一次排序。（如图）

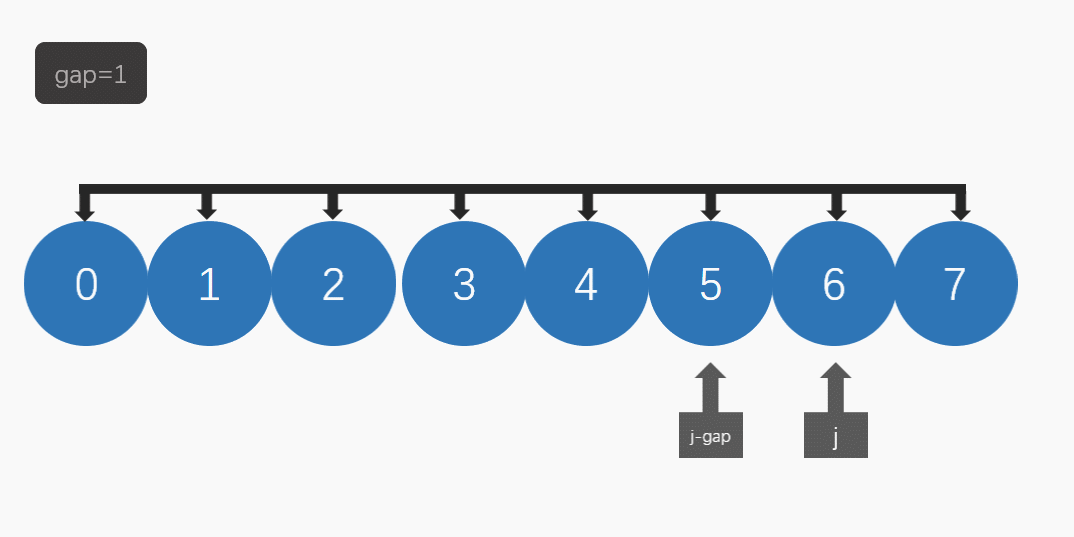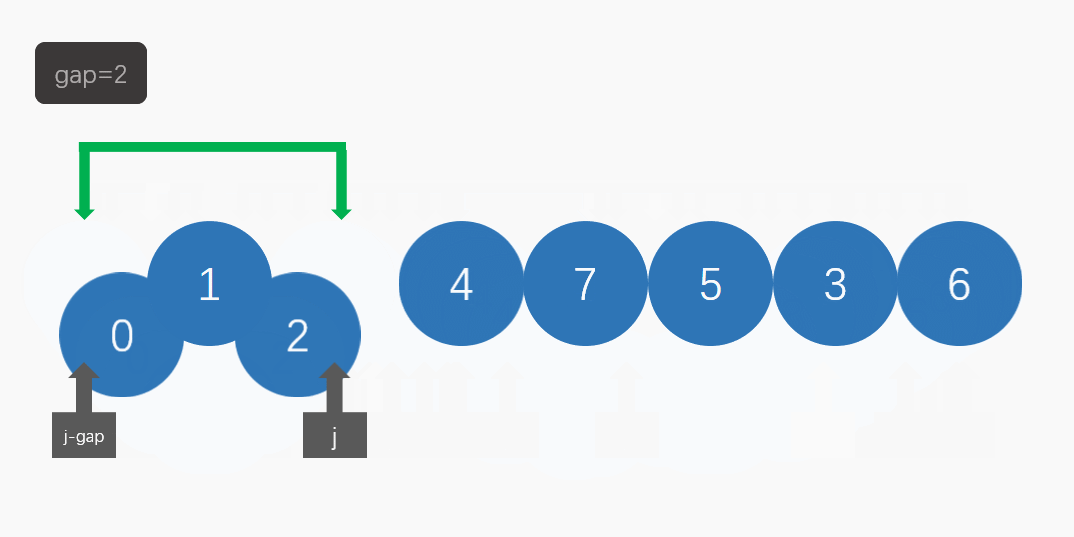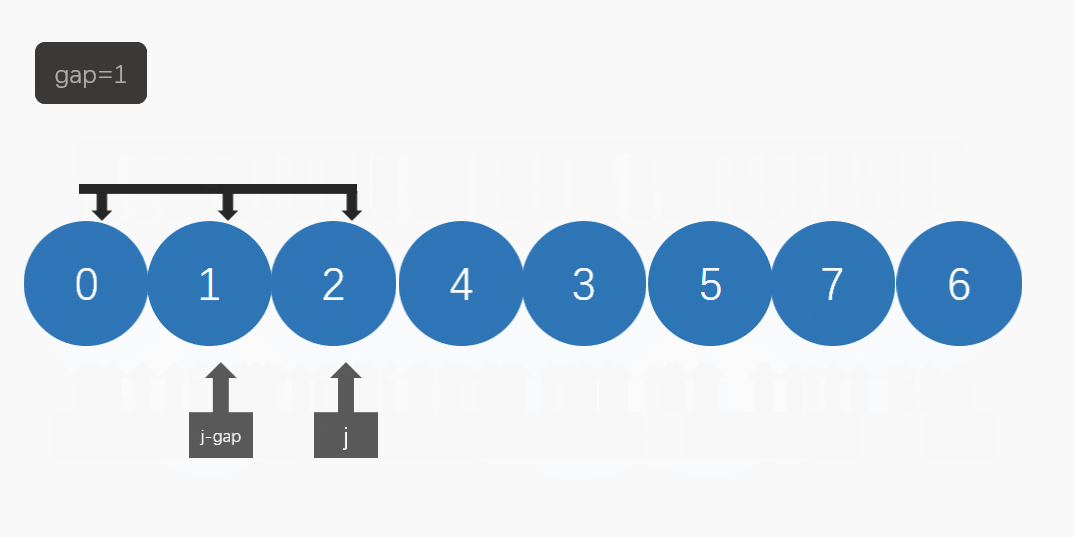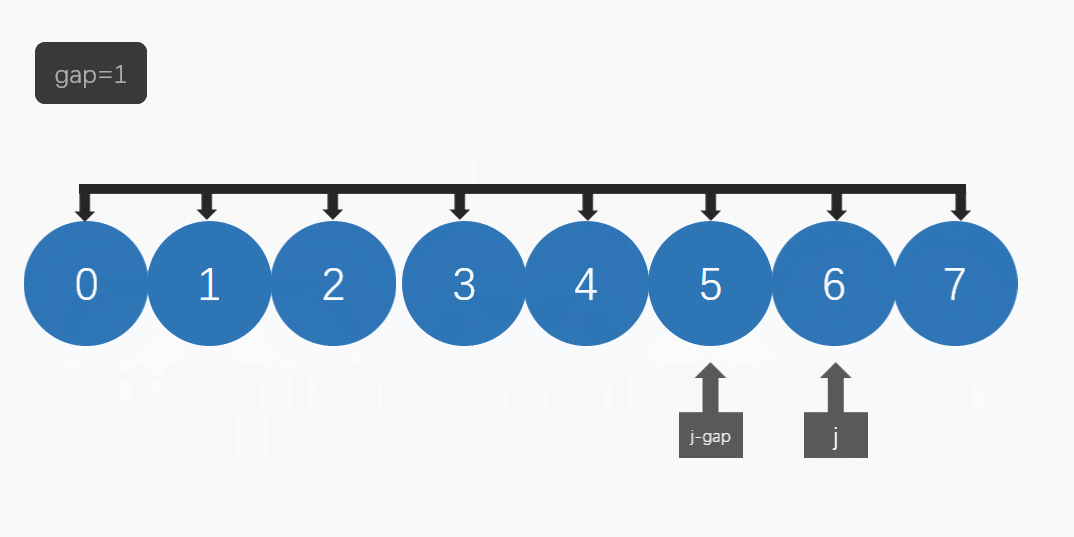
在希尔排序中，我们要引入gap（间隔）：

当gap不为1时，我们可以把它看做为一个预排序，先把数组变得比较有序。

然后当 gap为1时 就是直接 插入排序了。

因为插入排序对比较有序的数组排列效率更高，所以希尔排序就为先预排序，再直接插入排序。

预排序

我们先定义一个长度为5的逆序数组{5，4，3，2，1}，再来假设gap为3。

知周所众 众所周知插入排序再排逆序的数组时，时间复杂度为最坏的情况。 所以我们才要进行预排序。

经过预排序后数组，已经变得比较有序了，这对后面的直接插入排序是有好处的，提高效率。

Knuth增量序列

Knuth增量序列是希尔排序中使用的一种增量序列，它可以保证gap最后一定为1，

它的计算方式为：

gap = 1, 3, 9, 27, ...

其中gap的初始值为1，然后每次计算下一个增量值h时，都乘以3再加1，直到h大于等于数组长度的三分之一

Knuth增量序列的特点是在每次排序中能够更好地减少逆序对的数量，从而提高排序的效率。

该增量序列的选择是经验性的，并没有严格的数学证明，但在实践中已经被广泛接受，并被证实在大多数情况下都能够有效地改善希尔排序的性能

代码实现希尔排序

下面是使用实现希尔排序的代码：

#include<iostream>

using namespace std;

const int N = 1e6+5;

int n,arr[N];

void shellSort() {

    int gap = 1;// 使用Knuth增量序列，gap = 1, 3, 9, 27, ...

    while (gap < n/3) gap = 3 * gap + 1;// 使用Knuth增量序列，保证gap最后为1

    while (gap >= 1) {// 逐步缩小增量直到1

        // 对每个子序列进行插入排序

        for (int i = gap; i < n; i++)

        for (int j = i; j >= gap && arr[j] < arr[j-gap]; j -= gap) swap(arr[j], arr[j-gap]);

        gap /= 3;// 缩小增量

    }

}

int main() {

	cin>> n;

	for(int i=0;i<n;i++) cin>> arr[i];

    shellSort();// 排序

    // 输出

    for (int i = 0; i < n; i++) cout << arr[i] << " ";

    return 0;

}

该代码使用了Knuth增量序列，h的初始值为数组长度的一半，然后逐渐减小h的值。

在每次循环内部，对每个子序列使用插入排序算法进行排序。最后输出排序后的数组。

总的来说，希尔排序可以应用于各种排序问题，并且在大规模数据下具有较好的性能。