Problem A. 最近公共祖先 ———2019.10.12

我亲爱的学姐冒险跑去为我们送正解

但是，，，，

阿龙粗现了！

cao,,

考场期望得分：20   实际得分：20

Problem A. 最近公共祖先 (commonants.c/cpp/pas)

最近公共祖先（Lowest Common Ancestor,LCA）是指在一个树中同时拥有给定的两个点作为后

代的最深的节点。
为了学习最近公共祖先，你得到了一个层数为 n + 1 的满二叉树，其中根节点的深度为 0，其他
节点的深度为父节点的深度 +1 。你需要求出二叉树上所有点对 (i,j),（i,j 可以相等，也可以 i > j）
的最近公共祖先的深度之和对 10 9 + 7 取模后的结果。
Input
一行一个整数 n 。
Output
一行一个整数表示所有点对 (i,j),（i,j 可以相等，也可以 i > j）的最近公共祖先的深度之和对
10 9 + 7 取模后的结果。

Notes
样例 1 解释：

树一共有 7 个节点（一个根节点和两个子节点） ，其中 (4,4),(5,5),(6,6),(7,7) 共 4 对的最近公共
祖先深度为 2，(4,2),(2,4),(5,2),(2,5),(5,4),(4,5),(2,2),(6,3),(3,6),(3,7),(7,3),(6,7),(7,6),(3,3) 共 14 对最
近公共祖先深度是 1 ，其他的点对最近公共祖先深度为 0 ，所以答案为 22 。

思路呢，，大概就是这样的：

算法1：

N<=10

直接暴力求树上两点的LCA

期望得分：20

（大概就是我的那20分吧）

代码~:

 #include<cmath>
 #include<cstdio>
 #include<iostream>
 using namespace std;
 int n;
 const int mod=1e9+;
 int deep[];
 long long ans;
 void dfs(int  i,long long t) {
     if(i>n) return;
     deep[t]=i;
     dfs(i+,t*),dfs(i+,t*+);
 }
 long long lca(long long i,long long j) {
     while() {
         if(i==j)break;
         if(i<j)swap(i,j);
         i/=;
     }
     return deep[i];
 }
 long long tot;
 int main() {
     freopen("commonants.in","r",stdin);
     freopen("commonants.out","w",stdout);
     cin>>n;
     tot=pow(,n+)-;
     dfs(,);
     for(int i=; i<=tot; i++)
         for(int j=; j<=tot; j++) {
             int k=lca(i,j);
             ans+=k;
             ans%=mod;
         }
     cout<<ans;
     fclose stdin;
     fclose stdout;
     return ;
 }

算法2：

代码：没得~

算法三：

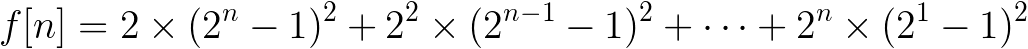
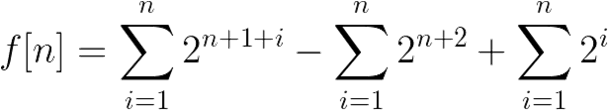
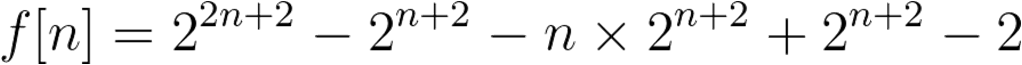
借土蛋 的代码一用

 #include <bits/stdc++.h>

 using namespace std;
 typedef long long ll;
 const ll mod = 1e9 + ;
 ll qpow(ll a, ll b){
     ll ret = ;
     for(; b; b >>= , a = a * a % mod){
         if(b & ) ret = ret * a % mod;
     }
     return ret;
 }
 ll n;
 ll f[];
 int main(){
     freopen("commonants.in", "r", stdin);
     freopen("commonants.out", "w", stdout);

     cin >> n;
     printf("%lld\n", (qpow(,  * n + ) - ( * n % mod + ) * qpow(, n) % mod + mod -  + mod) % mod);
     return ;
 }