[luogu P2054] [AHOI2005]洗牌

[luogu P2054] [AHOI2005]洗牌

题目描述

为了表彰小联为Samuel星球的探险所做出的贡献，小联被邀请参加Samuel星球近距离载人探险活动。

由于Samuel星球相当遥远，科学家们要在飞船中度过相当长的一段时间，小联提议用扑克牌打发长途旅行中的无聊时间。玩了几局之后，大家觉得单纯玩扑克牌对于像他们这样的高智商人才来说太简单了。有人提出了扑克牌的一种新的玩法。

对于扑克牌的一次洗牌是这样定义的，将一叠N（N为偶数）张扑克牌平均分成上下两叠，取下面一叠的第一张作为新的一叠的第一张，然后取上面一叠的第一张作为新的一叠的第二张，再取下面一叠的第二张作为新的一叠的第三张……如此交替直到所有的牌取完。

如果对一叠6张的扑克牌1 2 3 4 5 6，进行一次洗牌的过程如下图所示：

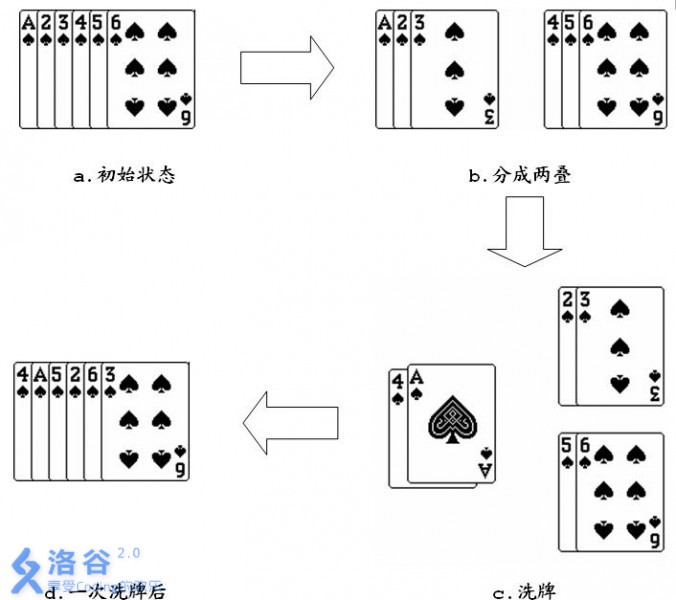
从图中可以看出经过一次洗牌，序列1 2 3 4 5 6变为4 1 5 2 6 3。当然，再对得到的序列进行一次洗牌，又会变为2 4 6 1 3 5。

游戏是这样的，如果给定长度为N的一叠扑克牌，并且牌面大小从1开始连续增加到N（不考虑花色），对这样的一叠扑克牌，进行M次洗牌。最先说出经过洗牌后的扑克牌序列中第L张扑克牌的牌面大小是多少的科学家得胜。小联想赢取游戏的胜利，你能帮助他吗？

输入输出格式

输入格式：

输入文件中有三个用空格间隔的整数，分别表示N，M，L

（其中0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数）。

输出格式：

单行输出指定的扑克牌的牌面大小。

输入输出样例

输入样例#1：

6 2 3

输出样例#1：

6

说明

0＜N≤10^10 ，0 ≤M≤10^10，且N为偶数

显然，设某张牌x当前位置为p，则洗牌一次后：

如果p<=n/2，则p变成2p；

如果p>=n/2，则p=(p-n/2)*2-1=2p-n-1=2p-(n+1)。

综上，可发现，无论怎样，p=2p%(n+1)。

则，m次后，原来在位置p的，现在在位置p*2^m%(n+1)。

但题目问我们位置l上是原来的几号，则设一个方程（是x号）x*2^m≡l (mod n+1)

然后相当于解一个二元一次方程，用exgcd就可以了。

code：

 #include<bits/stdc++.h>
 #define LL long long
 using namespace std;
 LL n,m,l,k,x,y,d;
 LL Qpow(LL b,LL p) {
     ) ;
     ) return b%n;
     LL t=Qpow(b,p/); t=(t*t)%n;
     ==?t:(t*b)%n;
 }
 LL exgcd(LL u,LL v,LL &x,LL &y) {
     ,y=; return u;}
     LL g=exgcd(v,u%v,x,y),t;
     t=x,x=y,y=t-(u/v)*y;
     return g;
 }
 int main() {
     cin>>n>>m>>l,n++,k=Qpow(,m);
     d=exgcd(k,n,x,y);
     x=(x%n+n)%n,d=l/d*x;
     cout<<d%n<<'\n';
     ;
 }