B. Mr. Kitayuta's Colorful Graph

 B. Mr. Kitayuta's Colorful Graph

 time limit per test

1 second

Mr. Kitayuta has just bought an undirected graph consisting of n vertices and m edges. The vertices of the graph are numbered from 1 to n. Each edge, namely edge i, has a color c_i, connecting vertex a_i and b_i.

Mr. Kitayuta wants you to process the following q queries.

In the i-th query, he gives you two integers — u_i and v_i.

Find the number of the colors that satisfy the following condition: the edges of that color connect vertex u_i and vertex v_i directly or indirectly.

Input

The first line of the input contains space-separated two integers — n and m (2 ≤ n ≤ 100, 1 ≤ m ≤ 100), denoting the number of the vertices and the number of the edges, respectively.

The next m lines contain space-separated three integers — a_i, b_i (1 ≤ a_i < b_i ≤ n) and c_i (1 ≤ c_i ≤ m). Note that there can be multiple edges between two vertices. However, there are no multiple edges of the same color between two vertices, that is, if i ≠ j, (a_i, b_i, c_i) ≠ (a_j, b_j, c_j).

The next line contains a integer — q (1 ≤ q ≤ 100), denoting the number of the queries.

Then follows q lines, containing space-separated two integers — u_i and v_i (1 ≤ u_i, v_i ≤ n). It is guaranteed that u_i ≠ v_i.

Output

For each query, print the answer in a separate line.

Sample test(s)

Input

4 5
1 2 1
1 2 2
2 3 1
2 3 3
2 4 3
3
1 2
3 4
1 4

Output

2
1
0

Input

5 7
1 5 1
2 5 1
3 5 1
4 5 1
1 2 2
2 3 2
3 4 2
5
1 5
5 1
2 5
1 5
1 4

Output

1
1
1
1
2

Note

Let's consider the first sample.

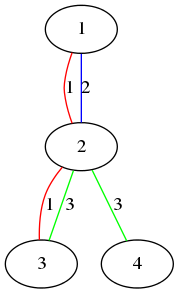The figure above shows the first sample.

• Vertex 1 and vertex 2 are connected by color 1 and 2.
• Vertex 3 and vertex 4 are connected by color 3.
• Vertex 1 and vertex 4 are not connected by any single color.

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <cmath>
 #include <map>
 #include <set>
 #include <stack>
 #include <queue>
 #include <string>
 #include <vector>
 using namespace std;
 const double EXP=1e-;
 const double PI=acos(-1.0);
 const int INF=0x7fffffff;
 const int MS=;

 int fa[MS][MS];
 void init()
 {
     for(int i=;i<MS;i++)
         for(int j=;j<MS;j++)
             fa[i][j]=j;
 }
 int find(int c,int a)
 {
     if(fa[c][a]==a)
         return a;
     return fa[c][a]=find(c,fa[c][a]);
 }
 void make_union(int c,int a,int b)
 {
     a=find(c,a);
     b=find(c,b);
     if(a==b)
         return ;
     fa[c][b]=fa[c][a];
 }
 int main()
 {
     int n,m,q,a,b,c;
     init();
     cin>>n>>m;
     for(int i=;i<m;i++)
     {
         cin>>a>>b>>c;
         make_union(c,a,b);
     }
     cin>>q;
     while(q--)
     {
         int ans=;
         cin>>a>>b;
         for(c=;c<=m;c++)
             if(find(c,a)==find(c,b))
                 ans++;
         cout<<ans<<endl;
     }
     return ;
 }