题解【[BJOI2012]算不出的等式】

题目背景emmm

\[\text{首先特判掉p=q时的情况（ans = }p^2-1\text{）}\]

\[\text{构造函数}f(k) = \left\lfloor \frac{kq}{p}\right\rfloor\]

\[\text{考虑这个函数}g(x)=\left\lfloor x \right\rfloor\text{的几何意义}\]

\[\text{他表示在平面直角坐标系中，横坐标为定值，纵坐标小于等于x的整点个数}\]

\[\text{好，那么我们继续来看f(k)，他表示所有横坐标为定值，纵坐标小于等于}\frac{kp}{q}\text{的数的个数}\]

\[\text{那么构造}t(k)=\frac{kq}{p}\text{，那么}\sum_{i=1}^{\frac{p-1}{2}}f(k)\text{的几何意义是：}\]

\[\text{所有横坐标}\in(1，\frac{p-1}{2})\;\text{的整数，纵坐标是整数的点数}\]

即

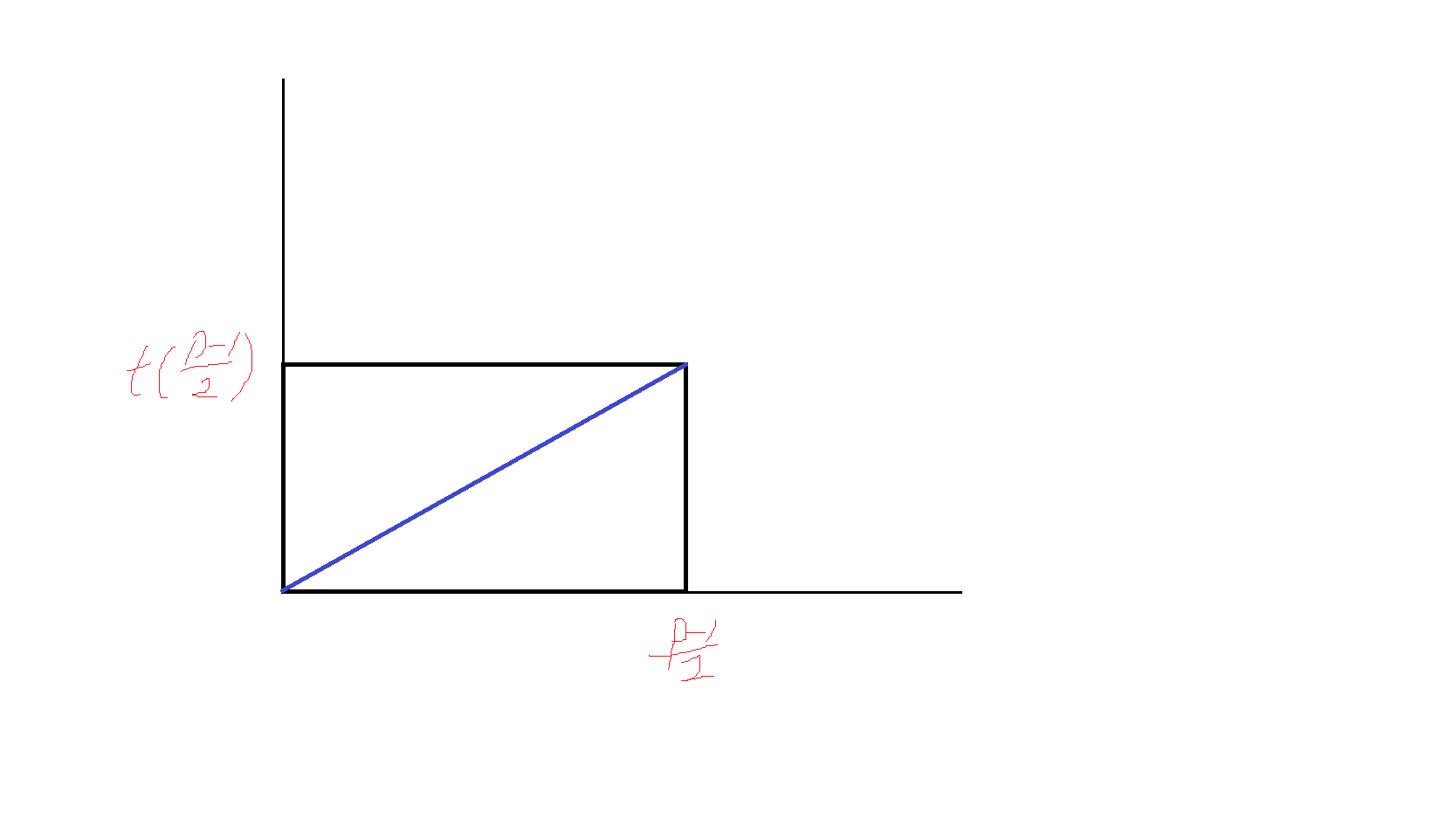
中蓝线以下部分中整点数
~

\[\text{又因为}\left\lfloor t(k) \right\rfloor_{max} = \frac{q-1}{2}\]

\[\text{所有只用考虑纵坐标在直线}\{(0,0),(\frac{p-1}{2},\frac{q-1}{2})\}\text{以下的整点}\]

\[\text{然后p,q互换同理}\]

\[\text{所以就是长方形ABCD}(A(0,0),B(0,\frac{p-1}{2}),C(\frac{q-1}{2},\frac{p-1}{2}),D(\frac{q-1}{2},0)\text{中整点个数}\]

\[\text{所以答案就是}\frac{(p-1)\times(q-1)}{4}\]

然后你就切了这道蓝题~