HDU 1143 Tri Tiling

链接：http://acm.hdu.edu.cn/showproblem.php?

pid=1143

Tri Tiling

Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/32768 K (Java/Others)

Total Submission(s): 2799 Accepted Submission(s): 1585

Problem Description

In how many ways can you tile a 3xn rectangle with 2x1 dominoes? Here is a sample tiling of a 3x12 rectangle.

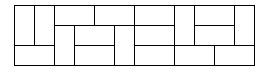
Input

Input consists of several test cases followed by a line containing -1. Each test case is a line containing an integer 0 ≤ n ≤ 30.

Output

For each test case, output one integer number giving the number of possible tilings.

Sample Input

2

8

12

-1

Sample Output

3

153

2131



Source



University of Waterloo Local Contest 2005.09.24



Recommend



Eddy



大意——3*n的长方形方格，用2*1的骨牌铺满。问：给定一个n。求解总的方案数。

思路——显然这是一道递推题目。非常明显地能够发现，当n为奇数时，是无解的。并且f(0)=1,f(2)=3,如今我们考察最后两列：假设最后两列铺满。则有3种方案，所以方案数为3*f(n-2);假设最后两列不铺满。则一定是后面四列组合。有2种方案，所以方案数为f(n-4)。以此类推。当n>=4时，f(n)=3*f(n-2)+2*f(n-4)+2*f(n-6)+···+2*f(0)。令2*m=n，则f(m)=3*f(m-1)+2*f(m-2)+···+2*f(0),f(m-1)=3*f(m-2)+2*f(m-3)+···+2*f(0),两式相减并整理得到,f(m)=4*f(m-1)-f(m-2)。从而。f(n)=4*f(n-2)-f(n-4),n>=4,并且n为偶数。又由于n最大为30，则直接递推就可以。



复杂度分析——时间复杂度：O(n),空间复杂度：O(n)

附上AC代码：

#include <iostream>
#include <cstdio>
#include <string>
#include <cmath>
#include <iomanip>
#include <ctime>
#include <climits>
#include <cstdlib>
#include <cstring>
#include <algorithm>
using namespace std;
typedef unsigned int UI;
typedef long long LL;
typedef unsigned long long ULL;
typedef long double LD;
const double PI = 3.14159265;
const double E = 2.71828182846;
LL num[31] = {1, 0, 3, 0};

void init();

int main()
{
	ios::sync_with_stdio(false);
	init();
	short n;
	while (cin >> n && n != -1)
	{
		cout << num[n] << endl;
	}
	return 0;
}

void init()
{
	for (int i=4; i<31; i++)
		num[i] = 4*num[i-2]-num[i-4];
}