caffe中的前向传播和反向传播

caffe中的网络结构是一层连着一层的，在相邻的两层中，可以认为前一层的输出就是后一层的输入，可以等效成如下的模型

可以认为输出top中的每个元素都是输出bottom中所有元素的函数。如果两个神经元之间没有连接，可以认为相应的权重为０。其实上图的模型只适用于全连接层，其他的如卷积层、池化层，x与y之间很多是没有连接的，可以认为很多权重都是０，而池化层中有可能部分x与y之间是相等的，可以认为权重是１。

下面用以上的模型来说明反向传播的过程。在下图中，我用虚线将y与损失Loss之间连接了起来，表示Loss必然是由某种函数关系由y映射而成，我们只需要知道这个函数是由后面的网络参数决定的，与这一层的网络参数无关就行了。

当我们知道了Loss对本层输出的导数dy，便能推出Loss对本层输入x及本层网络参数w的导数。

先推Loss对输入x的导数。由

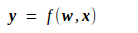
可知，y对x的导数如下，其中g为某种函数映射，它由上面的f唯一地确定，因而是一种已知的映射。

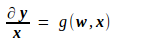
由此推出Loss对x的导数如下，其中h也为某种函数映射，也是由上面的f唯一地确定，是一种已知的映射。

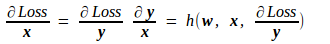
至于Loss对该层网络参数w的导数，由上述公式很容易得到

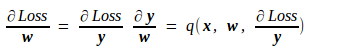
其中的p、q和g、h一样，都是由f确定的已知映射。

从上面的分析中可以看出，只要知道了Loss对本层输出的导数dy，就能计算出本层参数的梯度，并且求出Loss对本层输入x的导数dx。反向传播是从最后一层（损失层）向第一层（输出层）传播，损失层中Loss对输出的导数dy是能直接求取的，并且本层的输入恰是上一层的输出，因此这种计算可以由后向前地递推下去，这就是反向传播的大体过程。最后示意图如下图所示

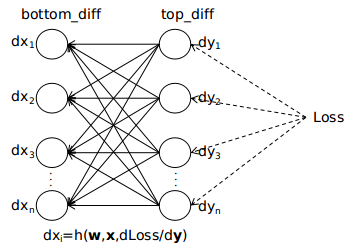
以上便是caffe实现反向传播的整体思路。对不同的层，由于前向传播的过程f不一样，所以对应的反向传播的过程p、q也是不一样的。在后面的章节中，我将结合源代码，分析ConvolutionLayer、PoolingLayer、InnerProductLayer、ReLULayer、SoftmaxLayer、SoftmaxWithLossLayer这几种层前向传播、后向传播的具体过程。